【脳葉強化】『小学生で解ける面積の問題②』 ひらめきラボ《0011》 ~算数の難問レベルは高校入試の問題になることも~
解答:
25cm2
解説:
オレンジ色のままだと、面積を求められないので、下の図のように点FからBCに平行な直線をひきます。
CDとの交点をIとおきます。

オレンジ色の面積は、上の図のように、ピンク色と青色に分けることができます。
次に、点FからABと平行な直線をひくと、上の図の青色(△FJI)と同じ図形ができます。(まだ同じどうか定かではない)
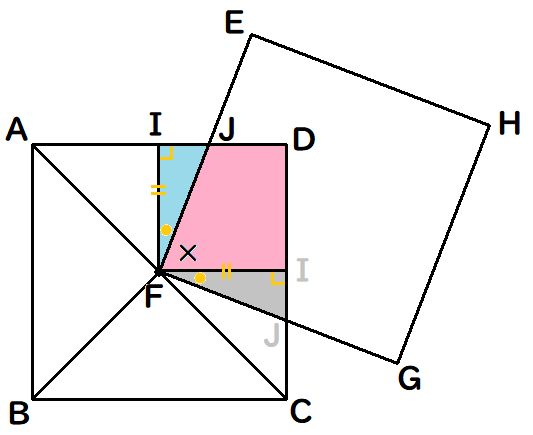
同じ図形になるために、三角形の合同であることをしめす必要があります。
△FIJと△FKLが合同であることを確認します。
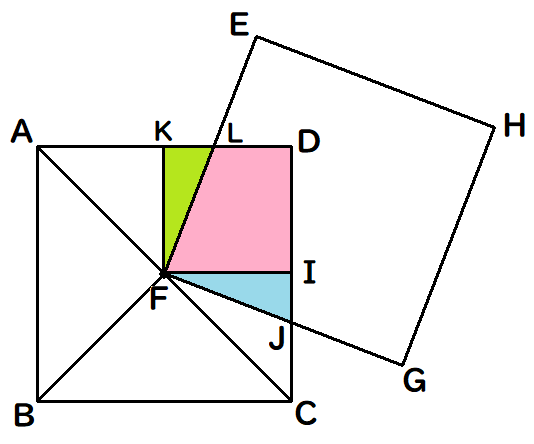
FIとFKは中心から90°になるように線を引いているので、長さは等しく、それぞれ90°で交わっている。
FI=FK・・・①
∠FIJ=∠FKL=90°・・・②

また、∠KFI=90°で、∠EFG=90°で、
∠IFJ=∠EFG-∠LFI=90°-×
∠KFL=∠KFI-∠LFI=90°-×
よって、∠IFJ=∠KFL・・・③
①,②,③より、1つの辺が等しく、その両端の角が等しくなっているので、△FIJと△FKLは合同といえます。
(1組の辺が等しくその両端の角がそれぞれ等しい)
よって求めたい面積は、下の右の図のように正方形IFIDになるので、5×5=25cm2となります。
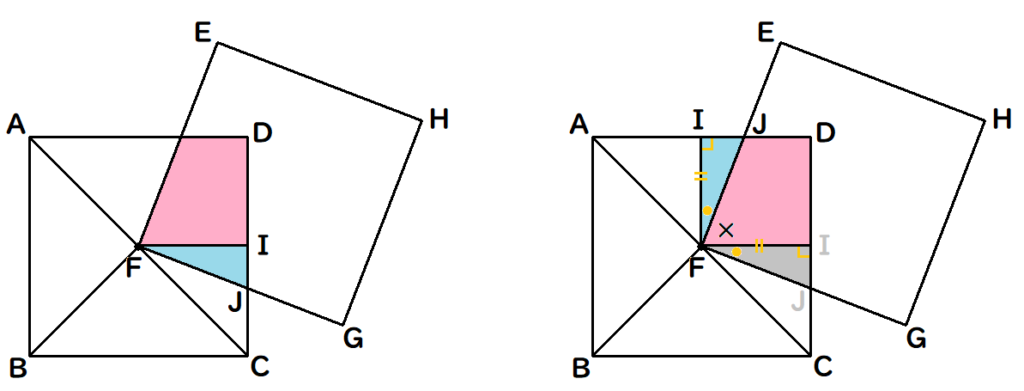

いかがでしたか。
答えは何となく、25cm2かなとわかると思いますが、きちんと説明するとなると少し難しいですよね。
上記のように合同になることを説明していますが、これは中学2年生で学習する合同の証明です。
算数の難問レベルは高校入試の問題になることも
今回の問題のように2つの正方形を重ねてというような問題が高校入試で出題されることがあります。
例えば、「下の図のように重ねた場合、FDの長さを求めなさい。」
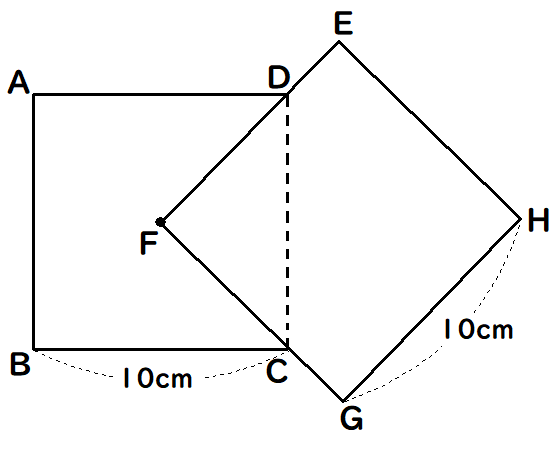
2問目で、今回の問題のように、合同の証明の問題と続くなどの流れで出題されます。
FDの長さ 答え
5√2 cm
(中3で学習する三平方の定理で教わります。)
算数の少し難易度の高い問題を解いていると、高校入試などで同じような問題に出会うことがあります。
いろいろな問題に触れておくと、解けなかった問題でも答えを見て何となく知っておくことで、次に同じような問題に出会ったときに解法に気づくことがあります。これは、経験を積んだことで起こる現象かもしれませんね。
小学校や中学校の修学旅行では、東大寺や仁和寺のような歴史的な場所に訪れます。これも、実際の経験が社会(歴史)の勉強において定着率を上げる効果があると思います。
「学習をした後に実際に経験する」ことも、「実際に経験した後に学習する」ことも、どちらも理解を深めるのに役立つと思います。実体験はやはり学習効果を高めるために重要そうですね。


