【脳葉強化】『ピンク色の面積は?』 ひらめきラボ《0002》
解答:
50cm2
解説:
内側(ピンク色)の正方形を45度くるりと回すと下の図のようになります。
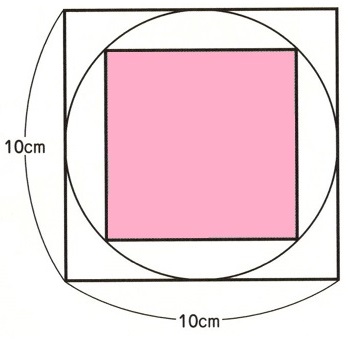
➡
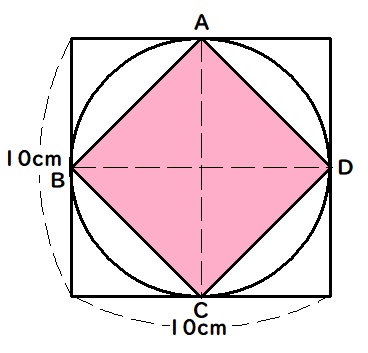
上の図のように、ピンク色の正方形の頂点をA、B、C、Dとすると、
正方形ABCDの対角線は、AC=BD=10cmとなります。
よって、ピンク色の正方形の面積は、10×10÷2=50cm2となります。
補足:
正方形の面積の公式は、「1辺×1辺」以外に「対角線×対角線÷2」でも求めることができます。
これは、ひし形の面積の公式ですね。

いかがでしたか。
中3の12月、1月頃に三平方の定理という単元があります。三平方の定理を教わると、この問題を三平方の定理で解きたくなるようです。
今回の問題とほぼ同じような問題が、実際の公立高校の入試でも出題されています。
上記の解説のように、「対角線×対角線÷2」をしていて、ピンク色の正方形を回転させる発想にいたれば、瞬時に解くことができます。
小学生の内は、この問題の解き方はこれしかないので、この発想に至るようですが、中3生は三平方の定理という手段でも解くことができます。
解く手段がいくつかあるとき、最短ルートで解ける方法に気づくことも大切です。(特に入試のような制限時間があるときは特に!)

こんな発想が思い付くのかな???
多くの受験生がこの問題を見たとき、三平方の定理を使いたくなると思います。
教わったばかりの手法ですし、受験勉強をしていれば三平方の定理を使う場面が多いですから無理もありません。
この問題のような工夫した解き方をする問題が初見であれば、三平方の定理を使うのもアリだと思います。
ただ、時間がかかってしまうので、ピンク色の正方形を回転させて考える解き方に気づきたいですね。
テスト中にひらめくためには、こういった問題を経験しておくことが重要です。
山梨県の公立高校入試の数学の問題では、今回のような考えをすれば瞬時に正解にたどり着ける問題が出題されています。
思考の選択肢の一つに、『図のまま解くのではなく、少し工夫をする』という考え方があることが大切です。
そのために、事前に類題などで経験をしておくことが重要です。
ひらめきや高度な発想と言われるものには、『0から1を生み出す』ものもありますが、『2×3を6にする』ような感覚に近いものもあります。
つまり、『2』や『3』といった経験があれば、『6』というひらめきを手に入れることができるのです。


