【脳葉強化】『三角形の底辺の比と面積の比』 ひらめきラボ《0022》 ~小・中学生のうちから育む「多面的・複合的に考える力」~
解答:
問題1:40cm2
問題2:48cm2
問題3:2cm
解説:
問題1
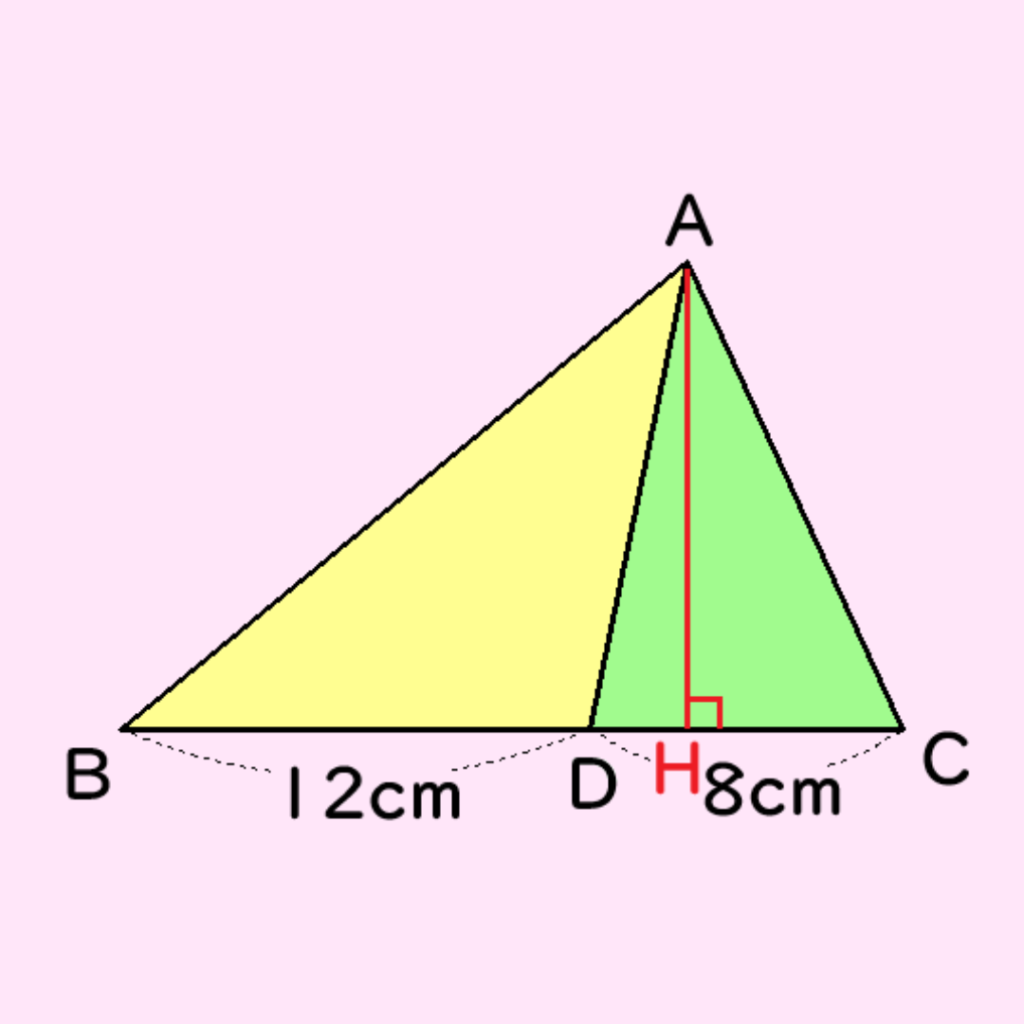
右の図のように、AからBCに垂線を下ろし、その交点をHとします。
AHは△ABCの高さになりますね。
AHは△ABDの高さでもあり、△ADCの高さでもあります。
AHがわかれば、求めたい△ADCの面積を求めることができます。
△ABD=60cm2なので、AH=60÷12×2=10cmとわかります。
(「×2」を忘れないように気を付けましょう)
よって、△ADC=8×10÷2=40cm2となります。
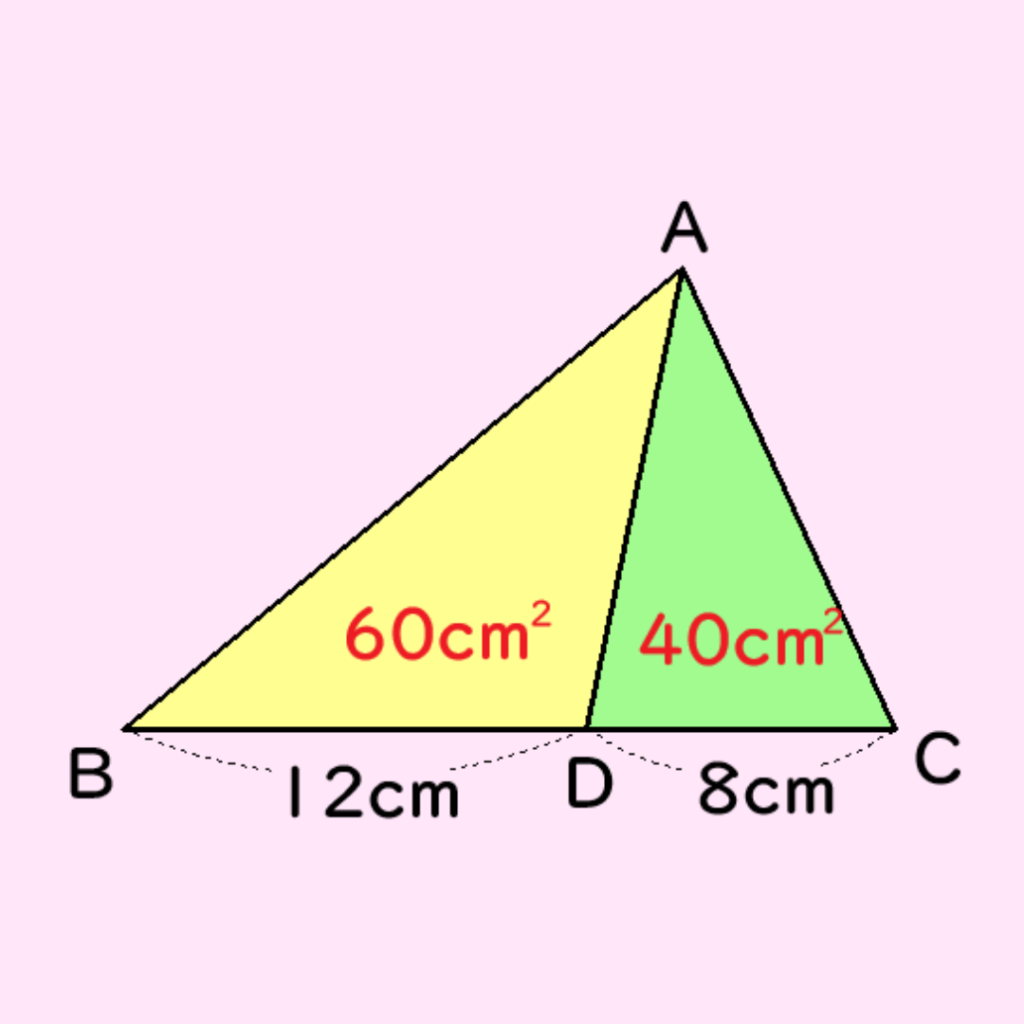
この問題のように、黄色(△ABD)と緑色(△ADC)は、高さが共通になっているので、
三角形の面積の比は、底辺の比と一致することになります。
実際に、
底辺の比は BD:DC=12:8=3:2
面積の比は △ABD:△ADC=60:40=3:2
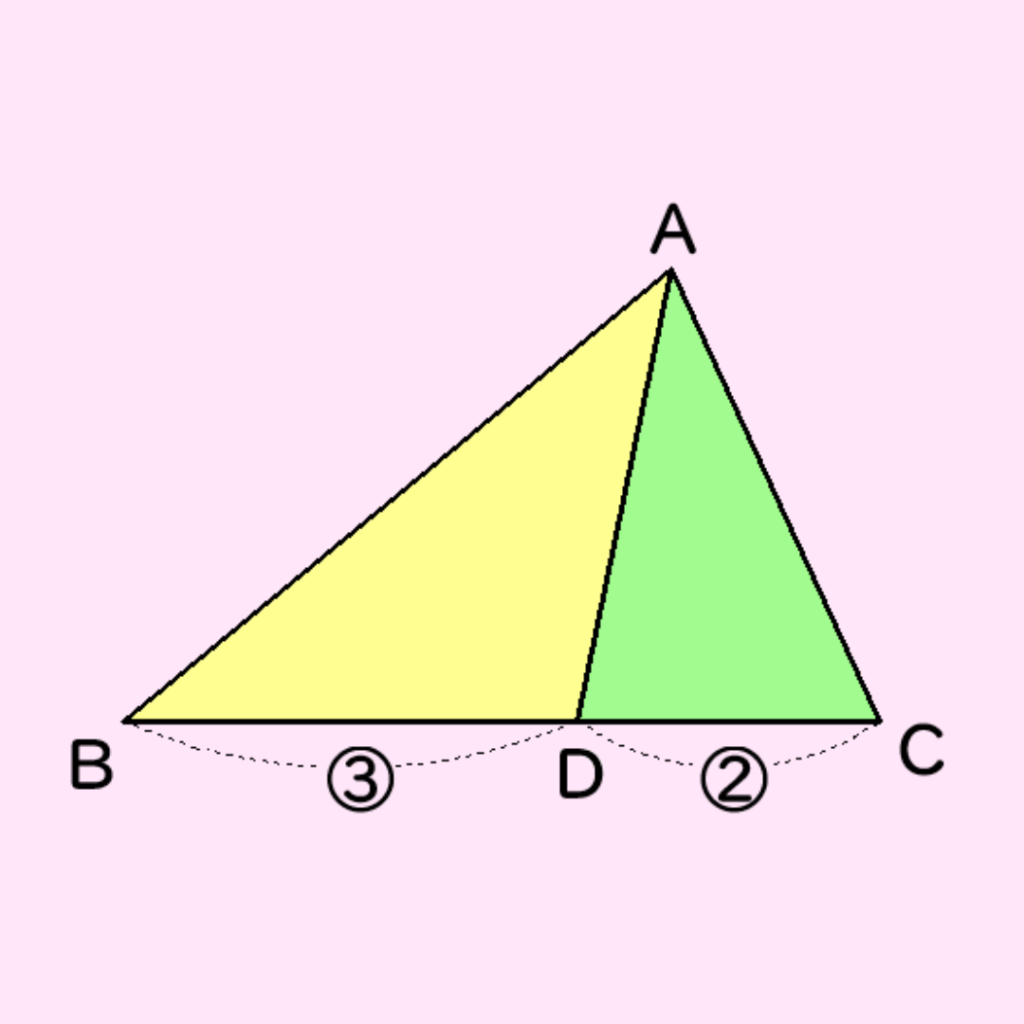
問題2
△ABD=72cm2で、上記の底辺の比と面積の比の関係より、
△ABD:△ADC=BD:DCとなる。
よって、72:△ADC=3:2で
△ADC=48cm2となる。
問題3
平行四辺形ABCDの面積は、48cm2で、対角線ACをひくと、△ABCの面積は24cm2となる。
△ABCにおいて、BE:EC=3:1より、△ABEと△AECの面積はそれぞれ、18cm2、6cm2であることがわかる。(下の図)
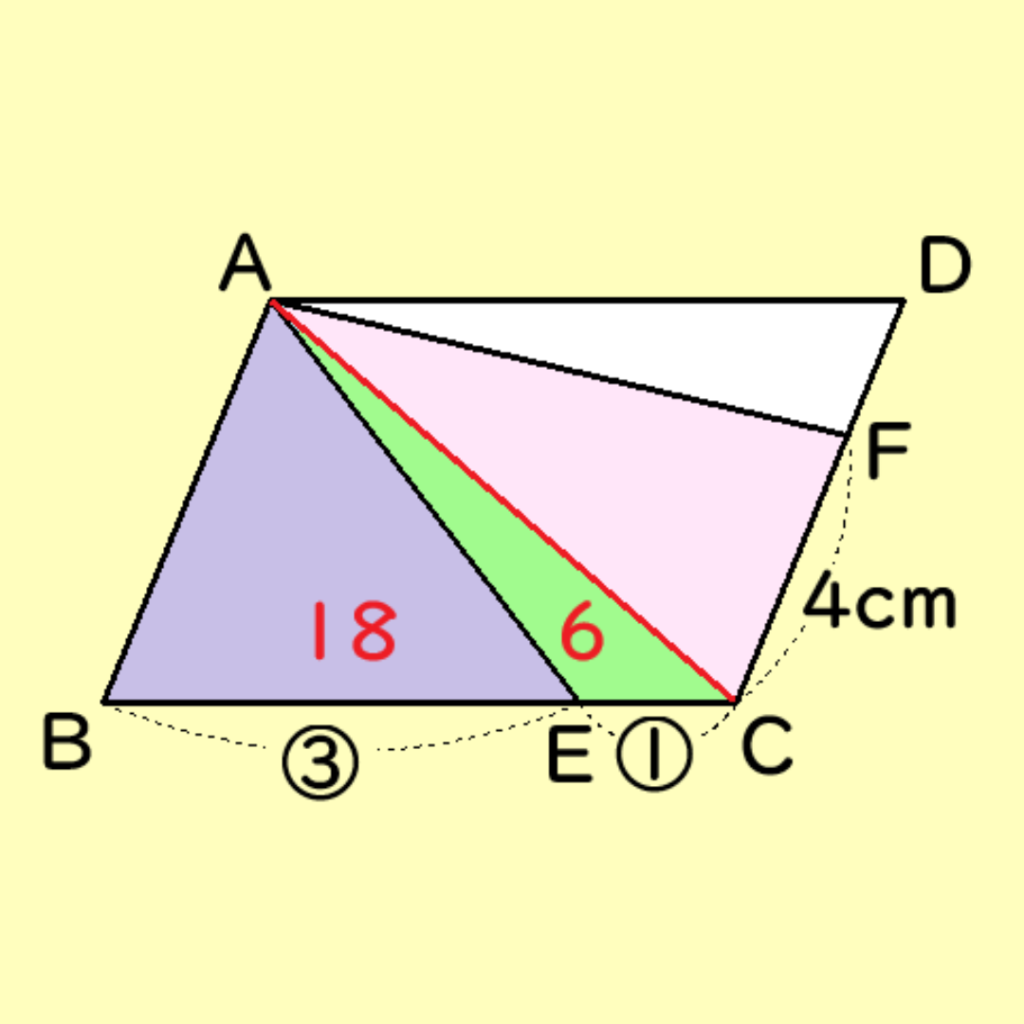
つぎに、四角形AECF=22cm2で、△AEC=6cm2より、△ACF=16cm2となります。(下の図)
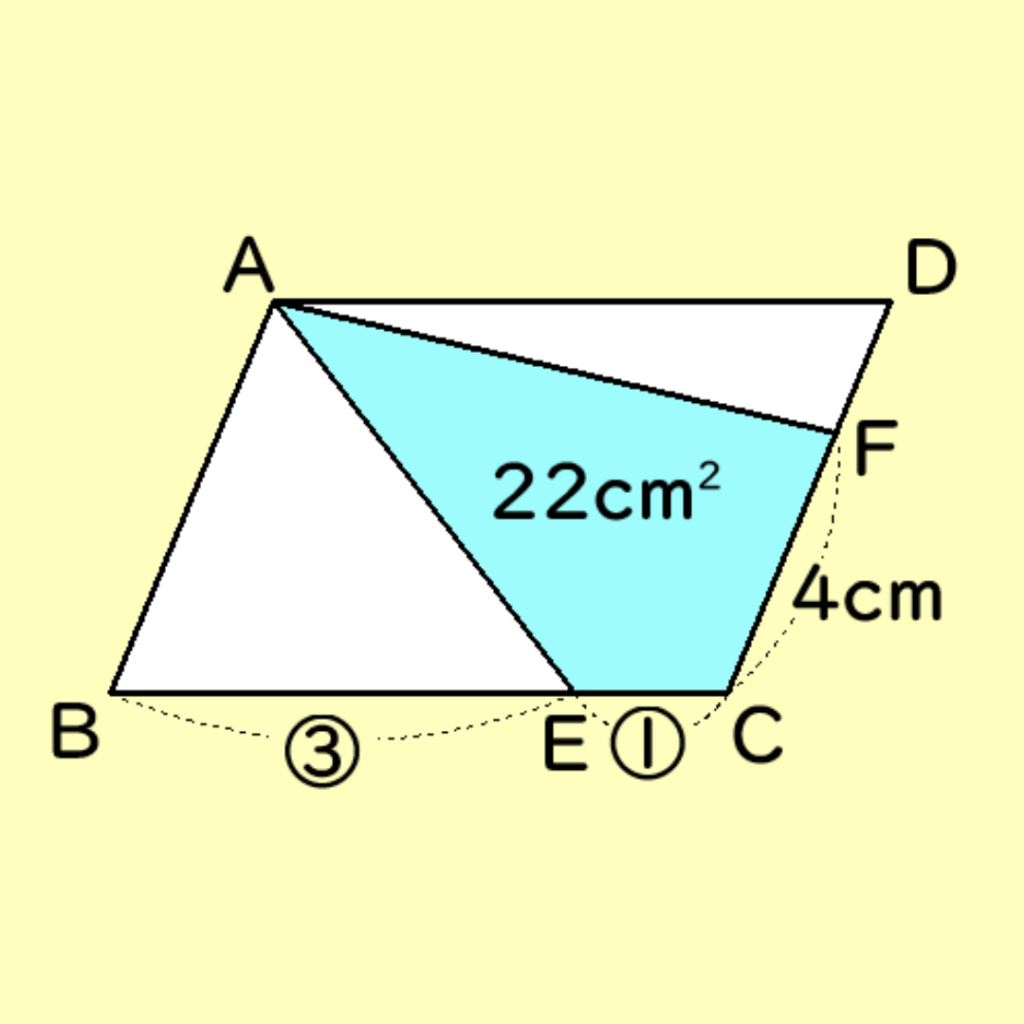
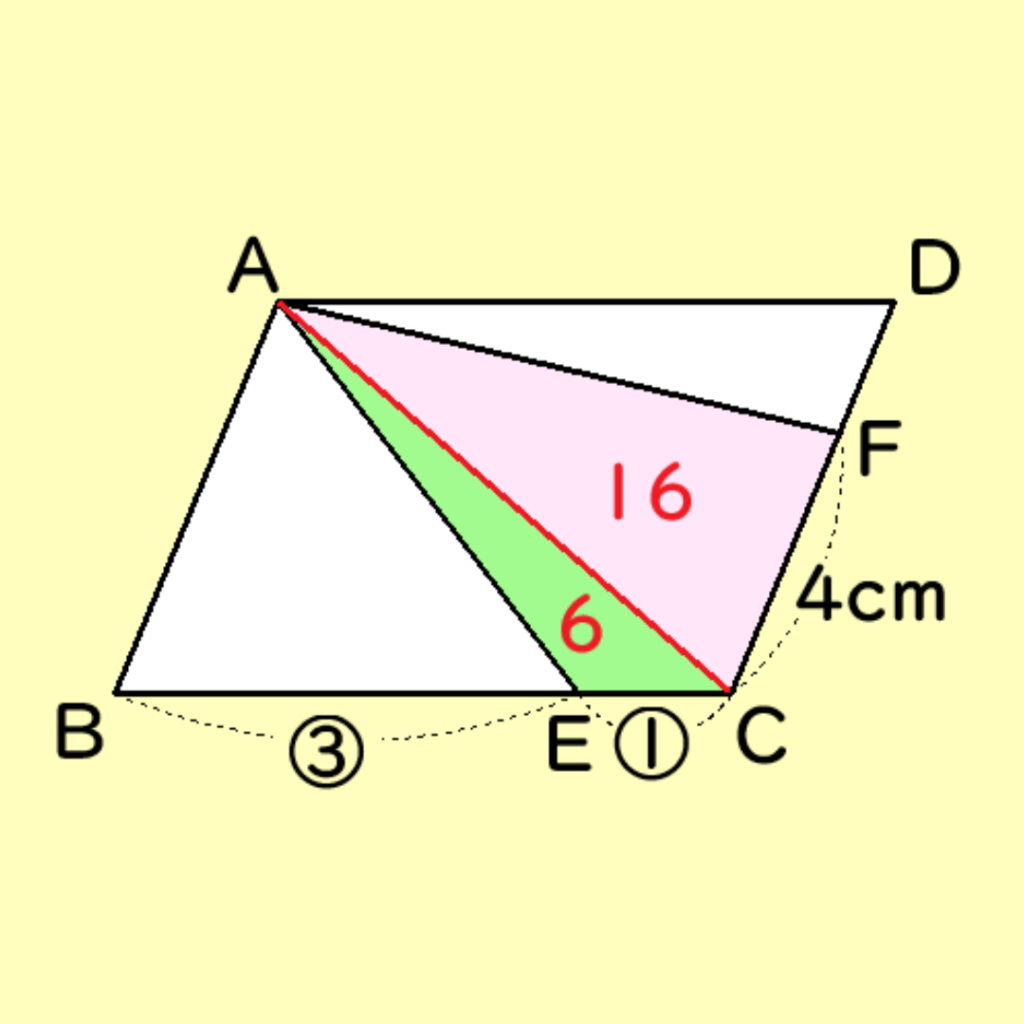
よって、△ACD=24cm2より△AFD=8cm2となることがわかる。
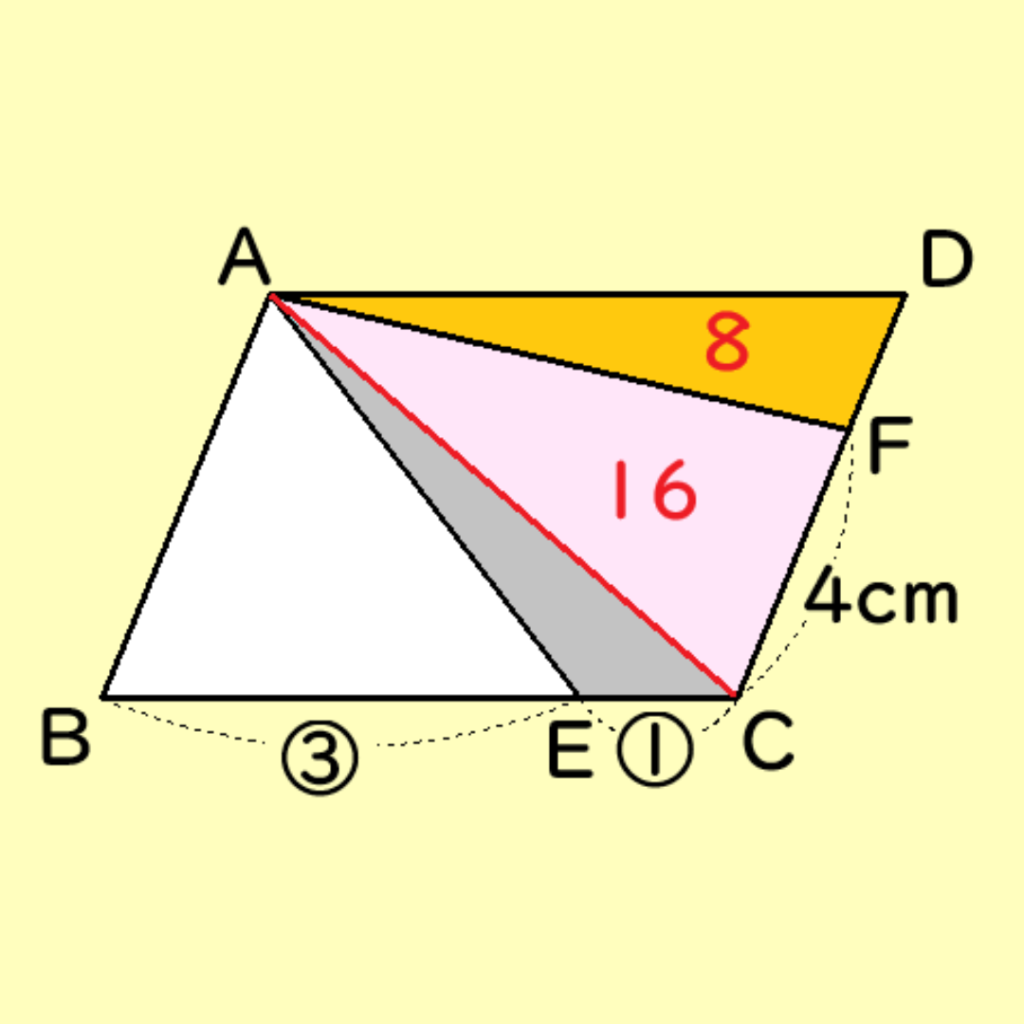
△ACFと△AFDの面積比が16:8=2:1となるので、 底辺の比CF:FD=2:1となる。
よって、4cm:FD=2:1で、FD=2cmとなる。

いかがでしたか。
「底辺の比と面積の比」の関係は、三角形の面積と比の単元を学習していれば、それほど難しい内容ではありません。
しかし、吉田高校理数科を志望している中学3年生の中にも、この関係を知らない生徒がいることがあります。
入試では、複数の学習内容を組み合わせて考える問題が出題されることがあります。
社会に出ると、課題を解決する際に一つの視点だけでは本質的な解決に至らないことが多々あります。
そのため、多面的・複合的に考える力が求められます。
今回のような問題は、そうした思考力を養う一助となるでしょう。
小学生・中学生のうちから育む「多面的・複合的に考える力」
私たちの社会は、ますます複雑化し、多くの情報があふれています。そんな中で求められるのが、「多面的・複合的に考える力」です。一つの視点だけでなく、さまざまな角度から物事を捉え、柔軟に思考する力は、学習だけでなく、将来社会に出たときにも大いに役立ちます。
しかし、この力は一朝一夕に身につくものではありません。小学生や中学生のうちから、日常生活や学習の中で少しずつ意識しながら育んでいくことが大切です。今回は、保護者の方がご家庭でできる具体的な方法をご紹介します。

1. 「なぜ?」を大切にする
子どもは日々、多くの疑問を抱きます。「なぜ空は青いの?」「なぜ勉強しなきゃいけないの?」といった質問に、すぐに答えを与えるのではなく、一緒に考える習慣をつけることが大切です。
例えば、「なぜ空は青いの?」と聞かれたら、「どうしてだと思う?」と問い返してみましょう。子どもが自分で考えることで、思考の幅が広がります。また、調べる習慣をつけることで、情報を取捨選択する力も養われます。
2. 異なる視点を持たせる
一つの出来事でも、人によって見方が異なることを理解することは、多面的な思考を育むうえで重要です。
例えば、ニュースや学校での出来事について、「もし立場が違ったらどう思う?」と話し合うことが効果的です。サッカーの試合でAチームが勝った場合、「負けたBチームの選手はどんな気持ちだろう?」と考えさせることで、相手の立場を想像する力が養われます。
3. いろいろな本を読む
本を読むことは、多様な価値観や考え方を学ぶ絶好の機会です。物語の登場人物の視点を考えながら読むことで、想像力や共感力が鍛えられます。
ノンフィクションや伝記、科学の本など、ジャンルを広げて読むことで、異なる分野の知識が増え、複合的に考える力が身につきます。親子で同じ本を読んで感想を話し合うのも良い方法です。
4. 日常生活の中で比較する
比較する習慣をつけることで、物事を多面的に捉える力が身につきます。
例えば、スーパーで買い物をするときに、「このジュースとあのジュース、どちらがお得だろう?」と考えさせるのも良い方法です。価格だけでなく、量や成分、健康面など、さまざまな視点から判断する練習になります。
また、歴史の勉強では、「もしこの出来事がなかったらどうなっていたか?」と考えさせるのも効果的です。
5. 問題解決型の遊びを取り入れる
ボードゲームやパズル、プログラミングなど、論理的思考を養う遊びを取り入れるのもおすすめです。
例えば、将棋やチェスは、相手の動きを予測しながら戦略を考える必要があります。また、LEGOやプログラミングは、試行錯誤しながら最適な解決策を見つける力を育てます。
このような遊びを通じて、「こうするとどうなるか?」を考える習慣が自然と身につきます。

6. 「一つの答え」だけにこだわらない
学校のテストでは、決まった正解を求められることが多いですが、現実の社会では必ずしも「正解」が一つとは限りません。
例えば、自由研究や作文では、「いろいろな答えがある」ということを意識させるとよいでしょう。「このテーマについて、他の考え方はあるかな?」と問いかけることで、柔軟な思考が身につきます。
7. 体験を通じて学ぶ
実際に体験することで、多くの気づきを得ることができます。
例えば、旅行に行ったときに、その土地の歴史や文化について調べるのも良い方法です。工場見学や職業体験など、普段できない経験をさせることで、さまざまな視点から物事を考える力が養われます。
まとめ
「多面的・複合的に考える力」は、学力だけでなく、将来社会で活躍するために欠かせない力です。この力を育むには、特別なことをする必要はなく、日常の中で少しずつ意識して取り入れることが大切です。
保護者の皆さんが、子どもたちと一緒に考え、対話することで、自然とその力は育まれていきます。ぜひ、今日からできることを取り入れてみてください。


