【脳葉強化】『平行四辺形と面積《小5レベル》』 ひらめきラボ《0028》 ~「思い出せた!」が増える勉強法~
解答:
15㎠
解説:
平行四辺形は対角線を引くと、できる三角形の面積は平行四辺形の面積の半分になります。
2つの三角形の面積は等しくなりますね。
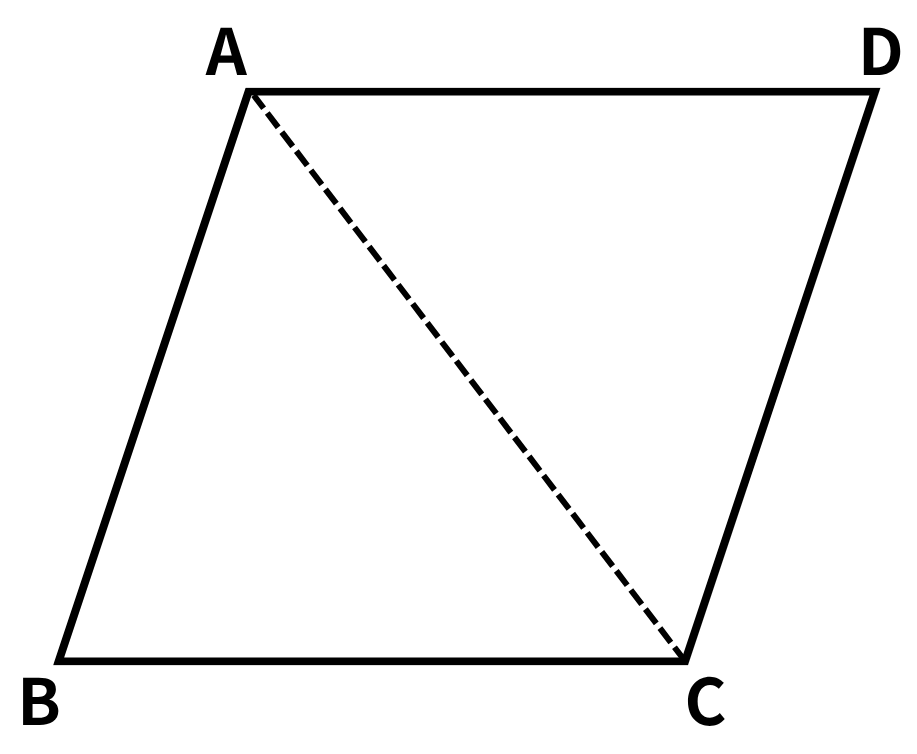
平行四辺形ABCDがあり、対角線ACを結ぶと、△ABCと△ACDの面積は等しくなります。
なぜなら、底辺をBC、ADとみると、BC=ADとなり、高さは共通になるからです。
小学5年生の三角形の面積を学習するときに教わりますよね。
今回の問題では、点Pを通るように、ADと平行なQR、ABと平行なSTを引きます。【下の図】
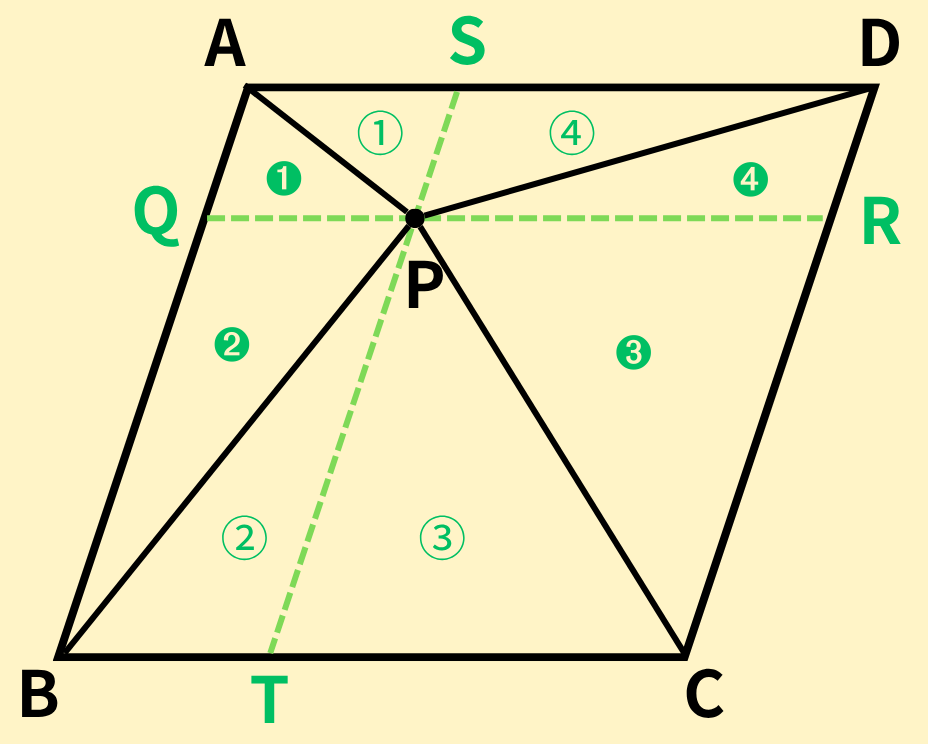
補助線を引くと、4つの平行四辺形AQPS、QBTP、PTCR、SPRDができます。
APは、平行四辺形AQPSの対角線になっているので、△AQPと△APSの面積は等しくなります。
➊=①と表しますね。
残りの3つの平行四辺形も同様に➋=②、➌=③、➍=④となります。
以上より、➊=①、➋=②、➌=③、➍=④より、
「①+②+③+④」=「➊+➋+➌+➍」となりますね。
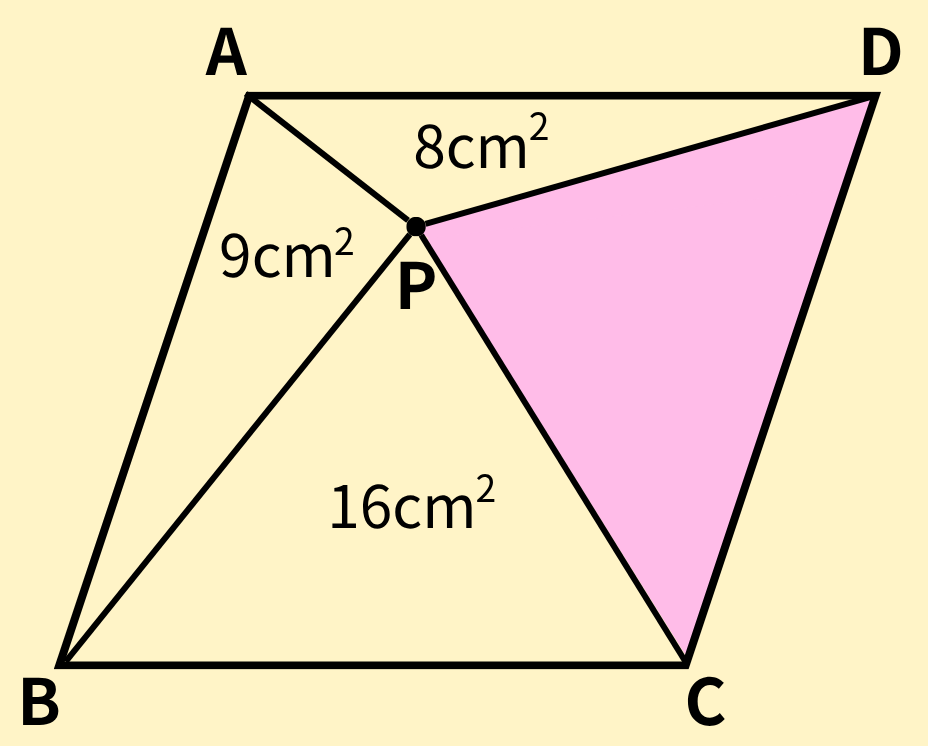
今回求めたい△PCD=➌+➍の部分になります。
①+②+③+④=8+16=24㎠より、
➊+➋+➌+➍=24㎠となり、➊+➋=9㎠なので、➌+➍=24-9=15㎠となります。
平行四辺形の内部の点Pと面積の関係
今回の問題のように、平行四辺形の内部に点Pを取ると、以下の関係性があります。
△APB+△PCD=△APD+△PBC
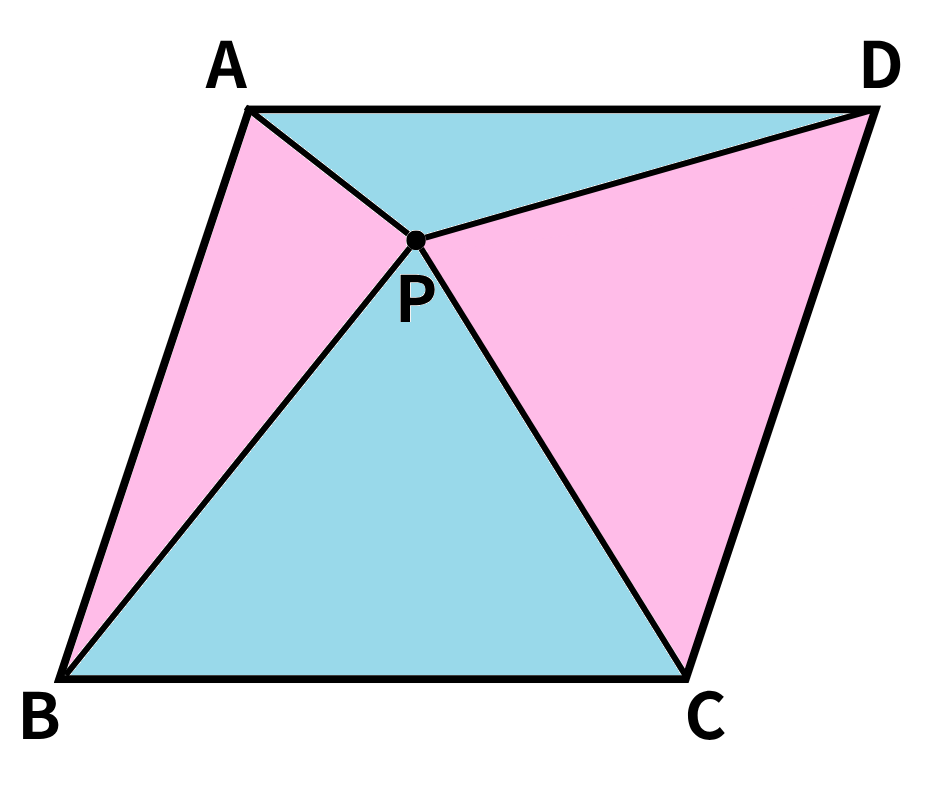
証明自体は、問題の解説にあるように、「①+②+③+④」=「➊+➋+➌+➍」となることが理由ですね。
点Pが平行四辺形の内部にあれば、どこにあってもこの関係性は成り立ちます。

いかがでしたか。ひと工夫して面積や角度を求める問題は、中学受験勉強をしているとよく見かけると思います。中学で学習する内容でも、今回のような考え方をする問題もあります。
これまで身につけた知識で問題が解けるようになるには?
「この問題、見たことある気がするけど…思い出せない」
そんな経験、誰しも一度はあるのではないでしょうか。
テストや入試では、知っているはずの知識を“使える状態”にしておくことが大切です。
では、どうすれば「学んだことを活かして問題が解ける」ようになるのでしょうか?
今回は、そのための考え方と具体的な方法をご紹介します。
◆ 知識は「使ってこそ」定着する
覚えた知識も、使わなければ忘れていきます。
例えば、自転車の乗り方。小さいころに練習して、何度も乗っているうちに自然と体が覚えましたよね。
勉強も同じです。公式や用語を「知っている」だけでは不十分。
「どんな場面で使うのか」「どう使うのか」まで理解し、練習することで、本当に“使える知識”になります。
◆ 問題を「分類」してみよう
学んだことを使えるようにするためには、次のようなステップをふむと効果的です。
① 問題を見たら「何の単元か」を考える
→ まずはその問題がどのジャンル・単元の知識を使うのかを特定します。
② 似た問題を思い出す
→ 「以前にこんなパターンを解いたことがあるかも」と記憶をたどるクセをつけましょう。
③ 使えそうな公式や考え方を挙げてみる
→ 選択肢のように「この知識か、あの知識か」と候補を出すと、引き出しが広がります。
このように、「記憶を探る」「知識を引き出す」練習を重ねることで、だんだんと問題に対して「これはこのやり方だ!」と反応できるようになります。
◆ 「練習のときに脳を使う」ことが大事
たとえば、学校のワークやプリントをただ埋めるだけでは、知識は定着しにくいかもしれません。
そこでおすすめなのが、「なぜそうなるのか」を自分の言葉で説明してみることです。
- なぜこの式になるのか?
- どんな場面でこの考え方を使うのか?
- 他にどんなやり方があるのか?
こうした問いを持ちながら練習すると、「ただの暗記」ではなく「活用できる知識」になります。
◆ 教える立場の人ができること
生徒に「知識を使えるようになってほしい」と願うなら、次のような声かけが効果的です。
- 「これはどんな単元の問題?」
- 「この前やった問題と似てない?」
- 「他のやり方でもできそう?」
こうした問いかけは、生徒の頭の中に「記憶の引き出し」をつくる手助けになります。
すぐに答えを教えるのではなく、「考える材料」を渡してあげましょう。
◆ まとめ:「覚える」から「使える」へ
- 知識は、使うことで定着する
- 問題を見たら「分類→想起→活用」を意識する
- 練習のときから脳を使う
- 教える人は「問いかけ」で思考をうながす
入試やテストで問われるのは、「覚えたかどうか」ではなく「使えるかどうか」。
日々の勉強の中で「自分の知識を引き出す練習」をしていくことで、問題を見たときに「これだ!」と思える力が育っていきます。


