【脳葉強化】『長さ2問』 ひらめきラボ《0032》 ~単元学習だけでは足りない!?~単元学習の落とし穴~~
解答:
第1問:9cm
第2問:12cm
解説: 第1問
使用する知識は、「縮図と拡大図(相似な図形)」です。
問題の図を下の図のように、△ABCと△EBDに分けます。
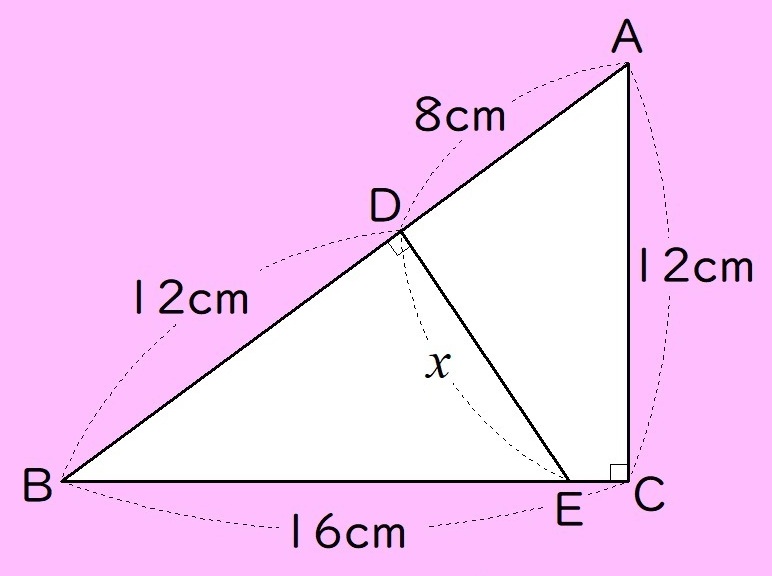
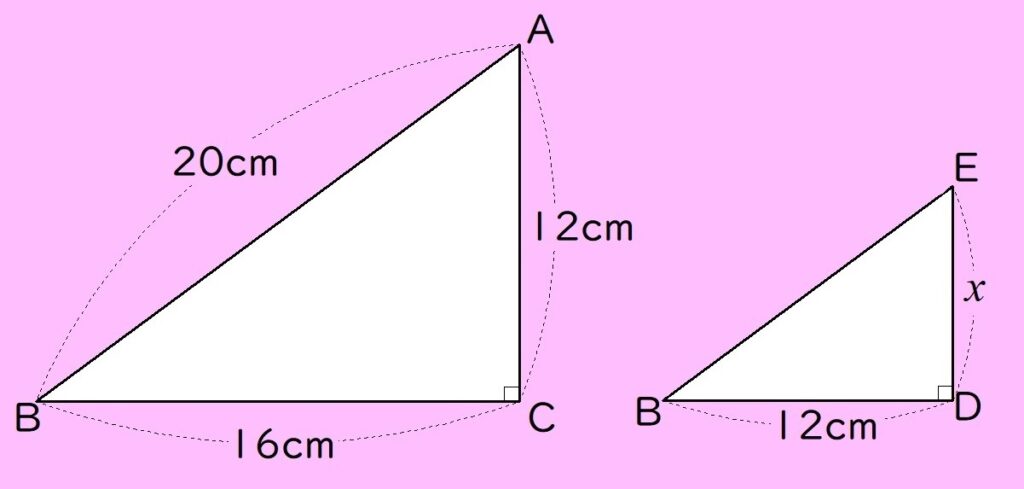
∠Bは共通な角で、∠ACB=∠EDC=90°より、2組の角がそれぞれ等しいので、
△ABCと△EBDは相似な図形(縮図と拡大図の関係)になります。
対応する辺の比が、「BC:BD=16:12」より、相似比は、4:3になります。
よって、求めたいDEの長さは、「4:3=12:DE」でこれを解くと、DE=9cmとなります。
解説: 第2問
使用する知識は、「線分の比と面積比」です。
台形ABED(ア)と△DEC(イ)の面積比は、ア:イ=7:3より、長方形ABCDの面積比は10となります。
BDの補助線を引くと、△ABD:△DBC=5:5となり、台形ABEDの面積比が7なので、△DBEの面積比は2となります。(下の図参照)
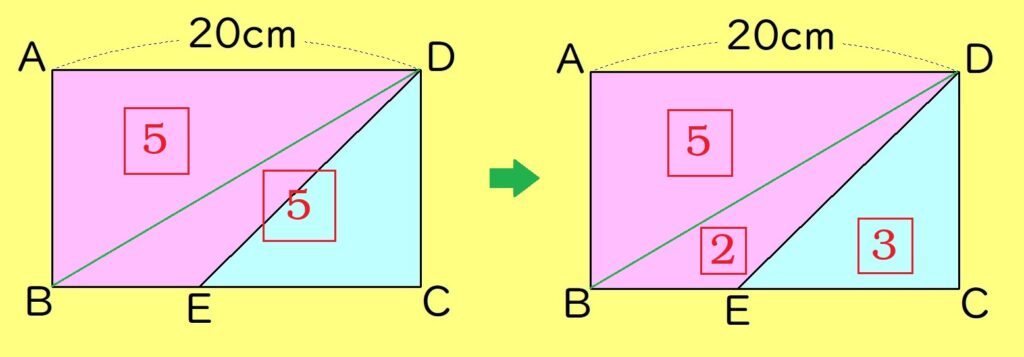
線分の比と面積比の関係より、△DBE:△DEC=2:3となるので、BE:EC=2:3となります。
よって、求めたいECは、「BC:EC=5:3」→「20:EC=5:3」で、EC=12cmとなります。

いかがでしたか。
第1問は相似な図形(縮図と拡大図)、第2問は線分の比と面積比の関係や長方形の面積の関係などの知識を用いて解くことができます。
それに気が付けると、解き進めることが容易だったかもしれません。そこに気づけるようになるために、単元学習だけではなく、総合問題などを解く必要があります。小学生のころのテストは単元テストだったので、まずまず得点が高かった生徒でも中学生になり、定期テストや到達度テストといった単元をまたいだテストになると得点が低くなってしまう子は、普段の勉強のしかた、解く問題集などを変える必要があります。特に高校入試や大学入試などでは、問題を見たときにどの知識を使うか気づくことができなかったり、使う知識を間違えてしまったりと、正答に行きつかないということがよくあります。
単元学習だけでは足りない!?
テストで点数を取るために必要な力とは
学校の授業やワークで出てくる「単元ごとの練習問題」。
これをしっかり解けるようになるのは大切ですが、それだけでは定期テストや模試、本番の入試で高得点を取ることは難しいことがあります。
なぜなら、本番のテストは「どの公式を使えばいいのか」を自分で判断しないといけないからです。

単元学習の落とし穴
小学生のころは「分数」「小数」「割合」など、ひとつの単元ごとにテストがありました。
だから「習ったばかりの内容」だけを使えば解けるので、点数が取りやすかったのです。
ところが、中学生・高校生になると、定期テストや到達度テスト、模試、そして入試は複数の単元をまたいで出題されるようになります。
例えば数学なら、関数の問題に図形の知識が混ざっていたり、方程式の考え方を組み合わせる必要があったりします。
そのときに「どの知識を使えばいいのか」に気づけないと、途中で手が止まってしまうのです。
どうすれば気づけるようになる?
では、どうすれば「この問題はこの公式を使えばいい」と気づけるようになるのでしょうか?
答えはシンプル。総合問題や過去問を解くことです。
単元ごとに分かれた問題は「足の筋トレ」や「腕の筋トレ」のようなもの。
でも本番のテストは「全身を使ったスポーツの試合」のようなものです。
どんなに足が速くても、ボールを投げられなければ野球では勝てませんよね。
同じように、テストではいろいろな知識を組み合わせて使う練習が必要になるのです。

総合力をつける勉強法
では具体的にどうすればいいか、いくつか方法を紹介します。
- 学校のワークが終わったら、単元横断型の問題集に挑戦する
→ 定期テスト対策だけでなく、模試や入試にもつながります。 - 「解けた・解けなかった」で終わらせない
→ 解いた後に「この問題にはどんな知識が必要だったのか」を振り返る習慣をつけましょう。 - 模試や過去問を定期的に解く
→ 時間内に解く練習をすることで、本番の緊張感にも慣れます。 - 友達や先生に説明してみる
→ 「この問題はなぜこの解法を選んだのか」を口に出して説明すると、理解が深まります。

まとめ
単元学習は「基礎体力づくり」。
でも、それだけでは本番のテストで点数を取るのは難しいです。
大切なのは、「どの知識を使うのか気づける力」をつけること。
そのために、普段から総合問題や模試、過去問を活用して「考える練習」をしていきましょう。
そうすれば、定期テストや入試で「あ、この問題はあの公式を使えばいいんだ!」と自信を持って解けるようになりますよ。


