【過去問YN】R5(23)M6 山梨県公立高校入試 数学 大問6 図形
PDFでダウンロードしたい方は下のボタンをクリック
↓ダウンロードだけならこちら↓
令和5年度 山梨県公立高等学校入学者選抜学力検査問題 数学 大問6
解答・解説
解答
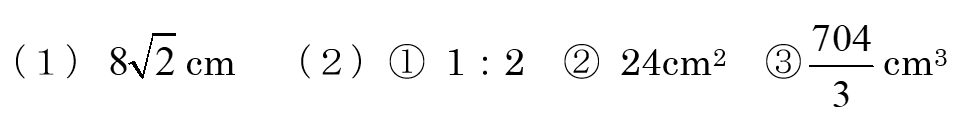
解説
解答
(1)
解説
(1)対角線AC結ぶ。
△ABCはAB=BCの直角二等辺三角形で、三平方の定理より求める。
90°・45°・45°の直角二等辺三角形より、1:1:の比を使うとより簡単ですね。
解答
(2)① 1:2 ② 24㎠ ③ ㎤
解説 ①
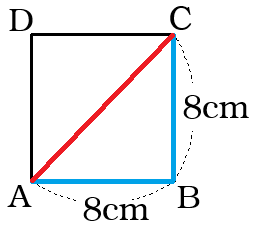
(1)よりAC=BD= cmで、BM=DM= cm。
条件のBP:PM=3:1、MQ:QD=1:3を利用すると、
MP=MQ= cmだから、PQ= cm。
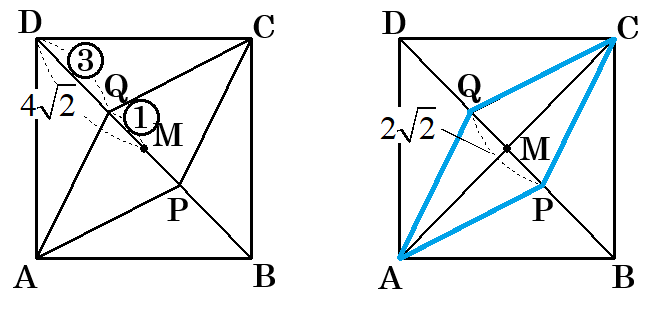
四角形APCQはひし形なので、× × =16cm2
四角形LIJKは正方形EFGHの半分なので、64÷2=32cm2
よって、16:32=1:2
I,J,K,Lは正方形EFGHの各辺の中点で、IJ=JK=KL=LIとなり、四角形IJKLは正方形とわかる。
下の図のようにIKとJLの交点をNとし、正方形KHLNに注目すると、オレンジ色と緑色の面積は等しくなります。他の場所も同様になるので、オレンジ色と緑色の合計の面積は等しくなり、緑色は正方形EFGHの半分になることがわかります。
解説 ②
(2) ② 下の図のように、平面AIJCを利用する。
四角形AIJCは図のような等脚台形なり、AI=との三角形で三平方の定理より、高さを求めることができる。高さは cm。
△AIMの底辺AM= cmとして、△AIM=×× =24cm2。
解説 ③
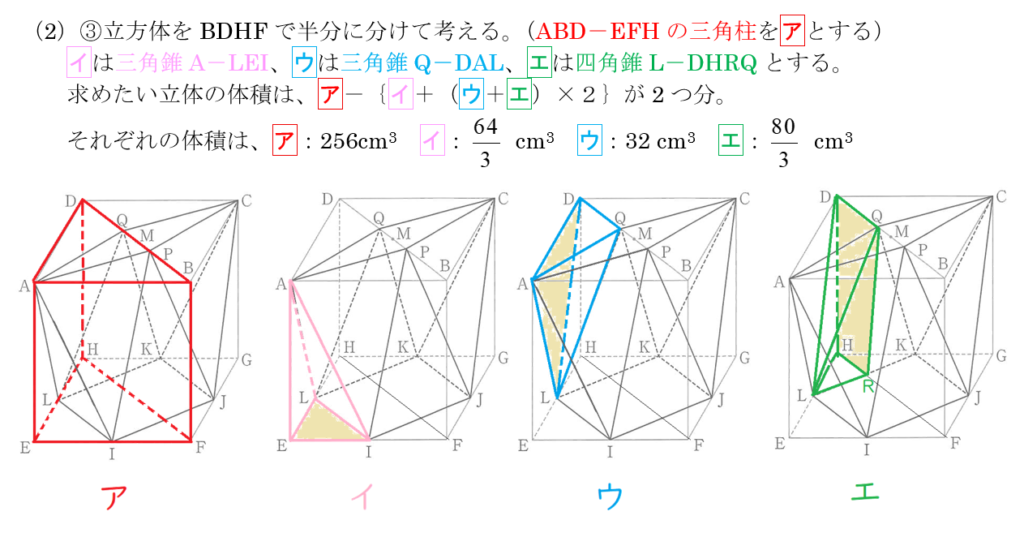

解説は以上です。
わかりにくい点があったら、学校の先生や塾の先生に補足してもらってください。
もし、まわりにこの問題が分からない友だちがいて、自分が理解できていたら、説明してみましょう。
人に説明できると、理解がより深まることがよくあります。(時間があるときだけで大丈夫ですよ)
本ページに掲載している入試問題および解答は、山梨県教育庁高校教育課の承認を得て掲載しています。
PDFでダウンロードしたい方は下のボタンをクリック
正答率
山梨県教育委員会HP参照
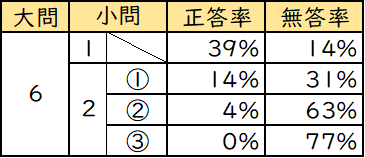
学力検査活用ガイドより

山梨県教育委員会HP 【学力検査活用ガイド】↓↓↓↓
https://www.pref.yamanashi.jp/documents/7061/r05kensakkkakatuyouguide.pdf
その他の教科、数学の他の大問の正答率、抽出調査・分析の概要等が確認できます。
本ページ閲覧やPDFのダウンロードは無料でご利用いただけますが、活動を続けるためにご支援をお願いしております。
もしこのページがお役に立ちましたら、今後の継続的な提供のためにご支援をいただけますと幸いです。
ご支援のお願い – 個別学習塾 LEAF

【LEAFの体験授業・お問い合せは】
・体験授業・ご入会・ご退会
・お問い合せ
【学力支援ページもご覧ください】
・【脳葉強化 ~ひらめきラボ~】 脳細胞フル回転!問題解決への挑戦!
・ 頑張る子のために~反復プリント~【ダウンロードページ】
・公立高校受験生応援ページ【山梨県公立高校入試 過去問】


