【脳葉強化】『小学生で解ける面積の問題③』 ひらめきラボ《0016》 ~高校入試での出題のされ方~
解答:
25cm2
解説:
下の図のように、点Aから辺EDに、点Cから辺BFにそれぞれ垂直な線を引きます。
その交点をP、Qとし、△APEと△CQFを切り取ります。

切り取った△APEと△CQFFを下の図のように辺AB、CDに重なる(接する)ように置きます。
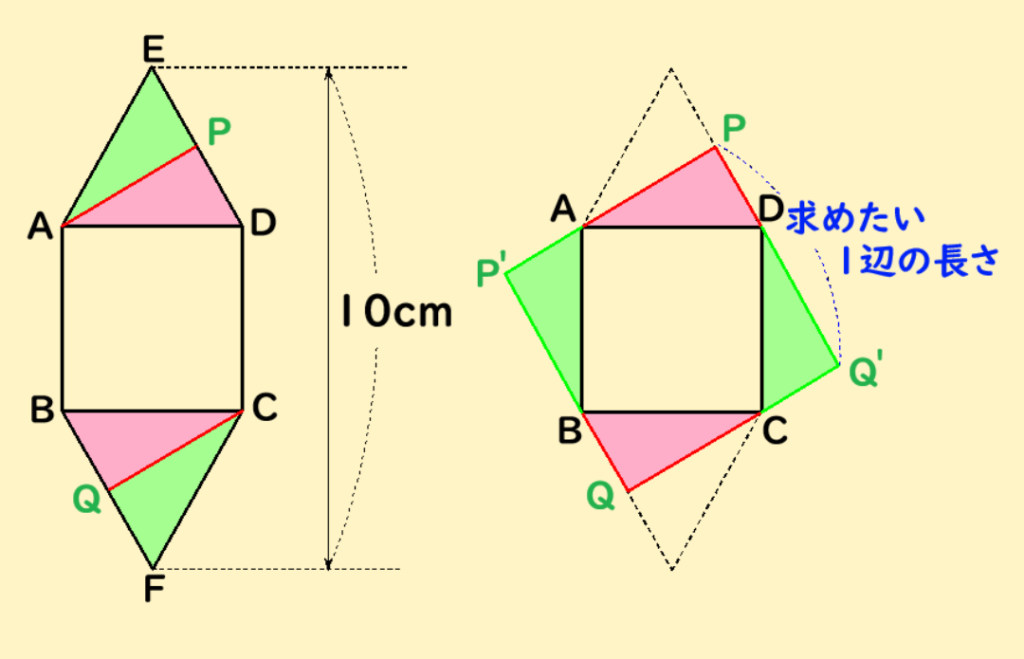
上の右図で、四角形PP’QQ’は正方形になることがわかります。
【四角形PP’QQ’が正方形になる理由】
四角形PP’QQ’において、
∠P、∠P’、∠Q、∠Q’ともに90°で、
PD=AP’=BQ=CQ’・・・①
PA=P’B=QC=CQ’・・・②
①、②より、
PP’=P’Q=QQ’=Q’P
よって、正方形となります。
PQ’の長さがわかれば、正方形PP’QQ’の面積=初めの図形の面積がわかります。
PQ’の長さを求めるために、初めの図形にもどります。
下の左図のように、正方形の対角線の交点をO、点EとOを結んだ長さEOを求めます。
FOを結ぶと、線対称な図形なので、EO=FOとなるので、EO=5cmとわかります。
EO=EM+MOで、MO=DMより、
EM+MD=(EO=)=5cm
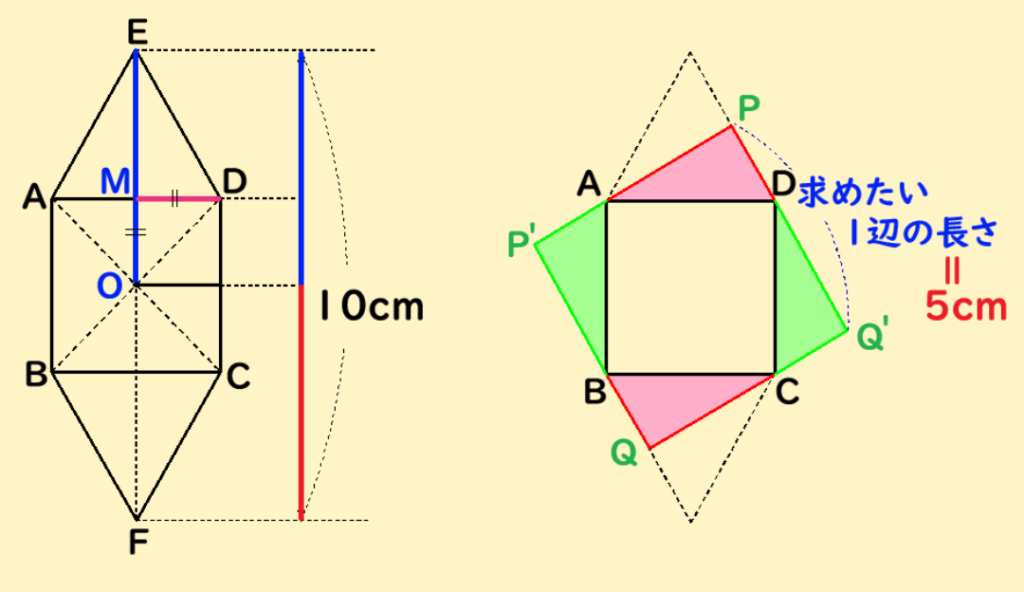
上の左の図の△EMDは、右の図の赤や緑の三角形と同じ図形です。
つまり、PP’=EM+MD=5cmとわかります。
よって、正方形PP’QQ’の面積=初めの図形の面積=5×5=25cm2となります。

いかがでしたか。
算数の図形の問題って、区切り方、面積の移動など工夫すると簡単に解けてしまう問題が多いですよね。
感覚的に解けることも大切ですが、「なぜ、それで求めることができるか?」を理解すると、
初見の問題でもひらめきにつながっていくと思いますよ。
高校入試で出題されるなら
公立高校入試では出題されないと思いますが、公立中学で学習していれば、理解できる解法です。
私立高校入試では、出題されてもおかしくない問題ですね。
チャレンジしてみてください。
では、問題を見てみましょう。
問題
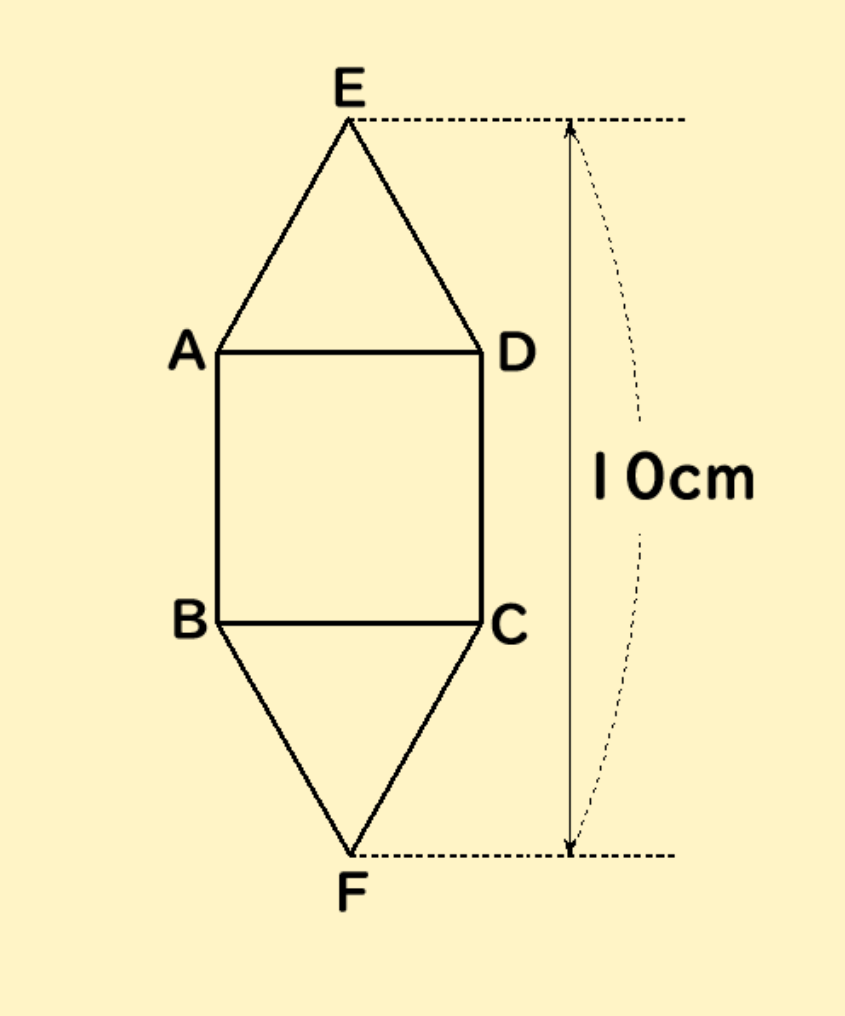
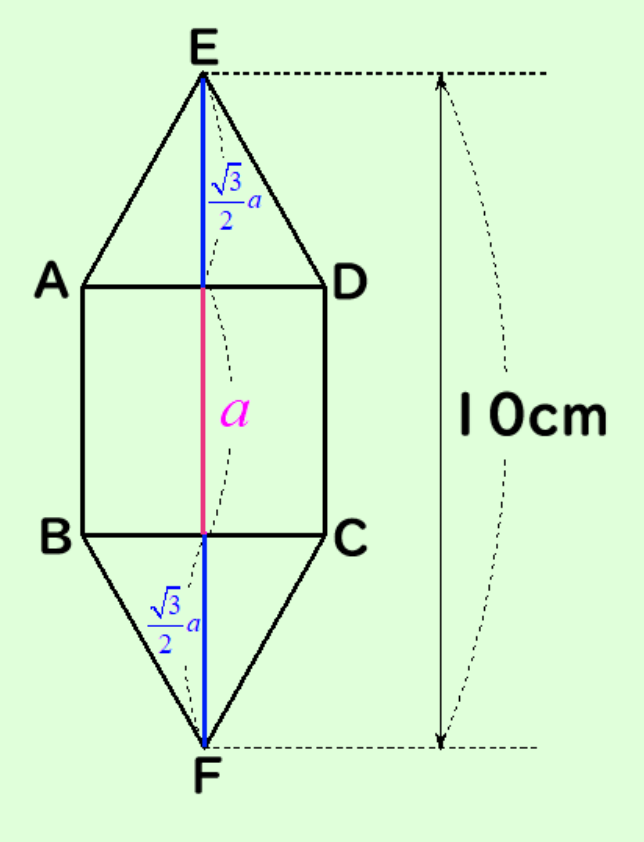
右の図は、正方形ABCDの上下に、それぞれの辺ADとBCを1辺とする正三角形が付いたものである。
点EとFの距離は10cmである。この時、次の問いに答えなさい。
(1)正方形ABCDの1辺の長さをa(cm)とするとき、EFの長さをaを用いて表しなさい。
(2)(1)を利用し、aの値を求めなさい。
(3)六角形ABFCDEの面積を求めなさい。
解答
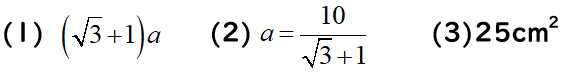
解説
(1)・(2)
下の図のように正方形の1辺をaとすると、正三角形の高さを求め、EFの長さで方程式を作れば、aの値を求めることができます。
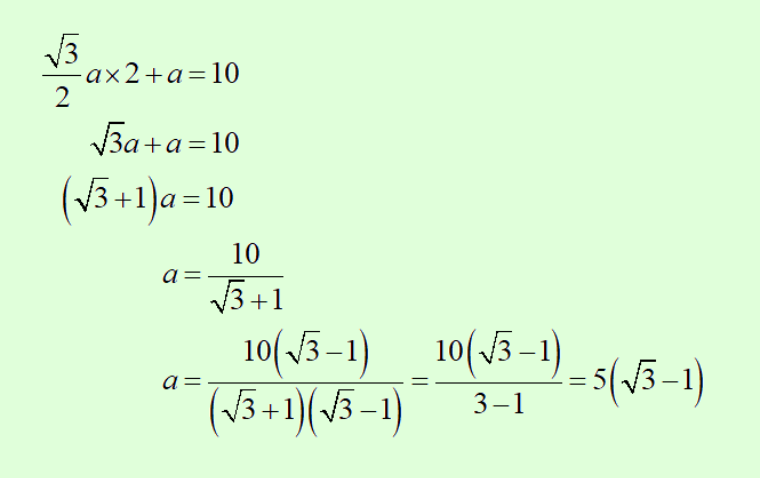
(3)
正方形・正三角形の面積をそれぞれ求め、(2)で求めたaの値を代入すれば求めることができます。


簡易的な説明となりましたが、もっと詳しく知りたい方は、コメントやお問い合わせいただければ、お答えいたします。


