【脳葉強化】『小学生で解ける面積の問題①』 ひらめきラボ《0004》
解答:
9cm2
解説:
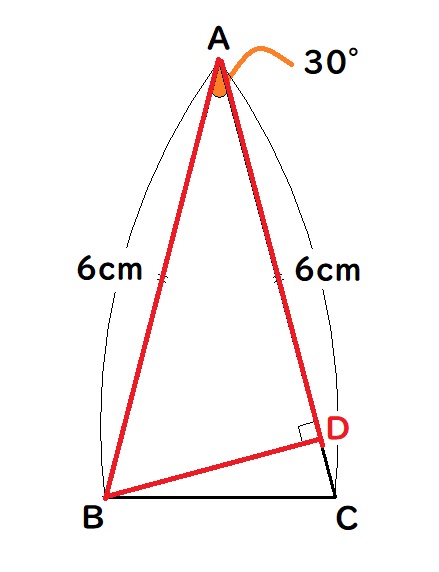
下の図のように、点BからACへ垂線(90度の線)を引き、その交点をDとする。
△ABD(三角形ABD)は、∠A=30°、∠D=90°なので、∠B=60°となる。
△ABDと同じ図形をもう一つ用意して下の図のように重ねると、△ABEができる。
この△ABEは正三角形になります。
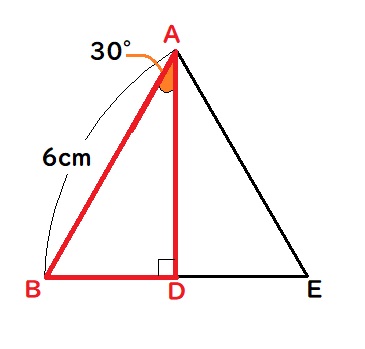
辺BDは辺BEの長さの半分になるので、BD=3cmとわかります。
元の図に戻ると、下のようになります。
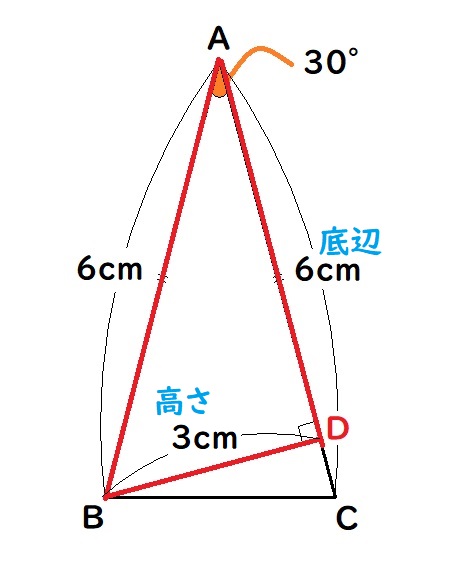
△ABCの面積は、底辺をAC=6cmすると、高さはBD=3cmとなります。
よって、6×3÷2=9cm2となります。

いかがでしたか。
補助線を引き、自分の知っている形をつくることがポイントですね。
図形は変えずに考える問題と、補助線を引き考える問題では、正答率がかなり違ってきます。
「知っている形」を見出せる補助線を引く能力を育てることが重要です。
学校のテストや入試問題は、みなさんがこれまでに学んだことを使って解けるように作られています。
知っていることをうまく組み合わせると、「そうか!」というひらめきが生まれ、問題が解けるようになります。
ただ、実際の社会ではそう簡単にはいきません。学校で習ったことだけでは対応できない問題や、思いがけない困難に出会うこともあります。
教科書に載っていない方法で解決しなければならないこともあるでしょう。
だからこそ、今の勉強がとても大切なのです。
テストや問題を解くときに、知っていることを組み合わせて新しい答えを見つける練習をしているのです。この力は、将来社会に出たときにきっと役立ちます。
今は難しく感じるかもしれません。でも、「知っていることを組み合わせて問題を解決する力」を身につけることが、みなさんの将来の成功につながることでしょう。今の勉強を大切にして、この力を少しずつ育てていってほしいですね。

ちなみに、中3の三平方の定理を教わっていても解き方は同じですね。BDをひくことができるかが勝負です。
高1の三角比を教わってしまえば、瞬時に解けてしまう問題でしたね。


