【脳葉強化】『中学校入試に出そうな4問』 ひらめきラボ《0035》 ~中学受験を検討している方へ〜
解答:
第1問:25.12cm2 (8π cm2)
第2問:4.5cm
第3問:22回
第4問:73分30秒
解説 第1問
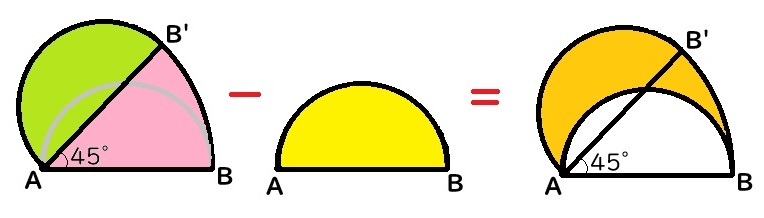
下の図のように、全体の面積(緑色+ピンク色)から半円の面積(黄色)を引いてを求めます。
緑色:半径4cmの半円の面積で、4×4×3.14÷2=25.12
ピンク色:半径8cmの8分の1の円の面積 (※360÷45=8)で、 8×8×3.14÷8=25.12
全体の面積は、25.12+25.12=50.24cm2
黄色:半径4cmの半円の面積で、4×4×3.14÷2=25.12cm2
よって、求めたい面積は、50.24-25.12=25.12cm2
別解
工夫したとき方は、上の解説を見て気づかれたかと思いますが、結局はピンク色の8分の1円の面積と一致します。
全体の面積(緑色+ピンク色)から半円の面積(黄色)を引いてを求めます。
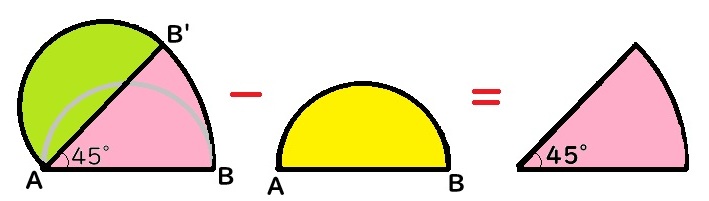
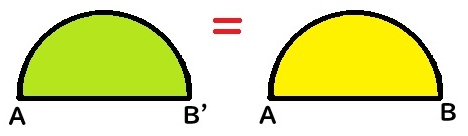
緑色の半円と黄色の半円の面積は等しいので、求めたい面積はピンク色の8分の1円の面積となりますね。
よって、8×8×3.14÷8=25.12cm2
解説 第2問
下の図のように、図形を分けて考えてみましょう。
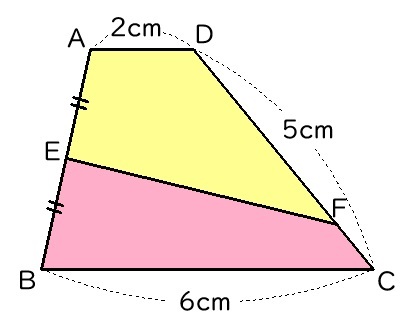
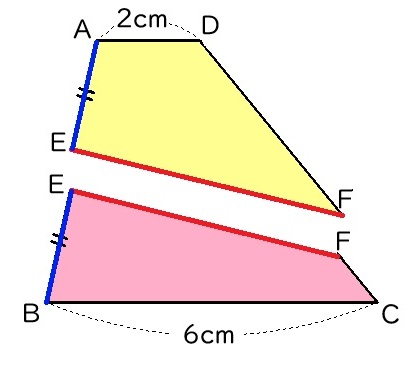
四角形AEFDと四角形EBCDの長さを考えます。
周の長さが等しいので、2つの図形の長さの違いを比べます。
長さの分かっていない部分を比べると、AE=BE、EF=EFとなるで、長さの違いはありません。つまり無視して残りの長さの違いを比べDFの長さを考えましょう。
黄色の図形のAD=2cmとピンク色の図形のBC=6cmより、4cmずれがあります。DC=5cmのうち、4cmのずれをなくすため、まず4cmを黄色の図形にふくめます。
そうすると、残り1cmを黄色とピンク色の図形に等しく分ければよいですよね。
よって、DF=4cm+0.5cm=4.5cm / FC=0.5cm と分ければ、周の長さが等しくなりますね。
よって、DF=4.5cmとなります。

4cmのずれがあるから、DF=4cm、FC=1cmと考えないように気をつけましょうね。
解説 第3問
0時からお昼12時になるまでに、長針と短針が何回重なるか考えてみましょう。

上の図のように1時台は1時5分ごろ、2時台は11分ごろ、3時台は17分ごろ・・・と各時間で1度重なりそうですね。
気をつけなければならないのは、11時台です。11時台のみ短針と長針が重なることなく、長針が一周し12時となります。
よって、0時~12時までは11回重なり、12時~24時までに11回となるので、1日で長針と短針が重なるのは、22回となります。
解説 第4問
「ユウヤの速さ」、「ユウヤの9800m地点での時間」、「ヒナの速さ」の順で必要な情報を求めていきます。
▶ユウヤの速さ
「スタートから36分後にゴール」とあるので、5kmの湖を2周、つまり10km=10000mを36分でゴールしたので、
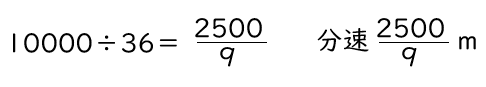
▶ユウヤの9800m地点での時間
ユウヤがヒナに追いついた地点は、ゴールの200m手前なので、ユウヤが9800m走った地点となります。そのときの時間を求めます。
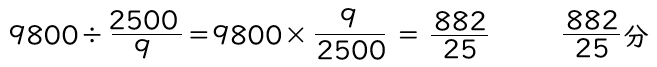
この時間は、ヒナの1周目の途中4800mを走った時間でもあります。
▶ヒナの速さ
次にヒナの速さは、4800mの道のりと、先ほど求めた 882/25 分で求めると、
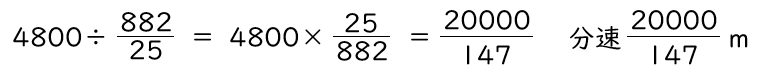
★ヒナがゴールするまでにかかった時間
湖2周10km=10000mを分速 20000/147 mで走るので、
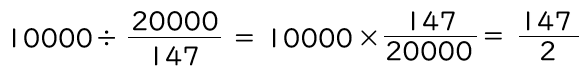
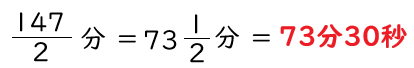
別解
ユウヤがヒナに追いついたときを考えると、
同じ時間あたりの距離、つまり速さの比を求めることができます。
2人の速さの比は、
ユウヤ:ヒナ=9800m:4800m=49:24 となります。
速さに比と時間の比は逆比となるので、 (※逆比は下記参照)
時間の比はユウヤ:ヒナ=24:49 となり、
ヒナの時間を求めると、24:49=36分:x分
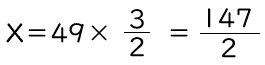
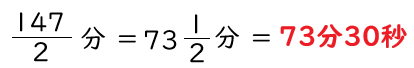

比を用いれば、ユウヤがヒナに追いついた時間を求めずとも他の情報を求めることができますね。また、その後の計算も簡単に解けますね。
速さと比の基本
- 道のりが同じ→ 速さと時間は逆比
- 速さが同じ → 道のりの比と時間の比は同じ
- 時間が同じ → 速さの比と道のりの比は同じ
外部サイト:速さと比の解説。速さと比の関係はイメージができればこんなに簡単!

いかがでしたか。
中学校入試の受験勉強をしている皆さんにとっては簡単な問題だったかもしれません。
中学受験勉強をしていない子たちは、あまり見慣れない問題だったかもしれませんが、いずれどこで出会うことになる問題になると思いますよ。思考のしかたを学ぶ良い機会になったと思います。
中学受験をするメリット・デメリット〜挑戦するお子さんと保護者の皆さまへ〜
中学受験を今後どうするか考えている方向けの内容で、ChatGPTに簡単にまとめてもらいました。
中学受験をするメリット
- 学習習慣が早く身につく
小学生のうちから計画的に勉強を進めることで、自然と「勉強の型」が身につきます。
中学・高校に進学したあとも、この基礎が大きな力になります。 - 環境が選べる
公立だけでなく、特色ある私立・国立中学を選ぶことで、お子さんに合った環境を整えることができます。
勉強に力を入れたい、部活動や校風を重視したい、将来の大学進学を見据えたいなど、目的に応じて選択肢が広がります。 - 目標に向かって努力する経験ができる
長期間の受験勉強は大変ですが、その分「努力すれば結果につながる」という実感を得やすいです。
合格・不合格に関わらず、この経験は一生の財産になります。
中学受験をするデメリット
- 時間やお金の負担が大きい
塾や家庭学習にかかる費用、送迎や生活リズムの調整など、保護者にとっても負担は少なくありません。 - 子どもへのプレッシャー
小学生にとって「受験」という言葉自体が大きな重圧になることもあります。
勉強が「義務」になってしまい、楽しさを失う危険性もあります。 - 家庭の時間が制限される
土日も模試や特訓で忙しくなり、家族での外出やゆったりとした時間が減ってしまうこともあります。
中学受験は…
中学受験は、親子で一緒に乗り越えていく大きなチャレンジです。
ときには成績に一喜一憂し、不安や焦りを感じることもあるでしょう。
でも、それだけお子さんと向き合い、未来を真剣に考えている証拠でもあります。
結果がどうであれ、ここまで努力してきた経験は必ずお子さんの成長につながります。
「頑張っているね」「あなたを応援しているよ」――その一言が、子どもにとって一番の力になります。
どうか保護者の皆さまも、ご自身をねぎらいながら、この期間を親子で大切に過ごしてください。
未来に向けて、一歩一歩前進していること自体が、すでに大きな価値なのです。


