【脳葉強化】『ころころ転がる図形』 ひらめきラボ《0037》 ~“全体”を見る目を育てよう~
解答:
問題①:12π(cm)・37.68cm
問題②:8π(cm)・25.12cm
問題③:(6+3√2)π (cm)
問題④:「半径2cmの円は、滑りながら動いている」
問題① 解説
求めたいPP’は、転がす円周の長さと等しくなる。
半径が6cmで直径12cmとなり、12×π=12π(cm)となる。
小学生→12×3.14=37.68cm
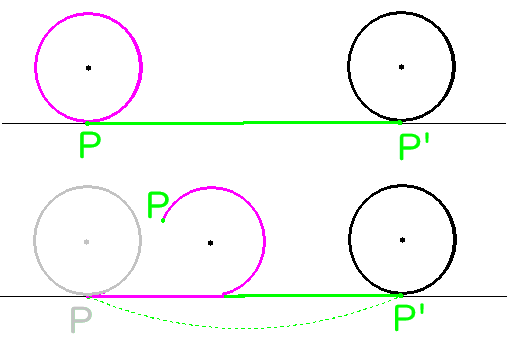
問題② 解説
点Aが動く場所を図に書き入れると下の図のようになります。
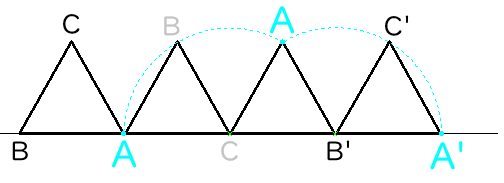
下の図のように
初めてAが動いたときのAの軌跡(動いたあと)は、ピンク色の中心角が120°のおうぎ形になりますね。
その後A’になるまでのAの軌跡は、青色のおうぎ形(中心角120°)ですね。
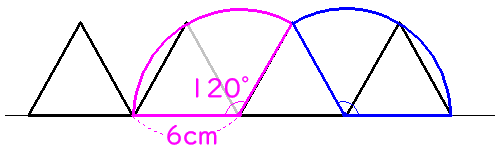
ピンク色と青色のおうぎ形をくっつけると、中心角が240°のおうぎ形になるので、弧の長さは、
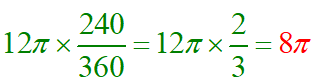
よって、8π(cm)となります。
小学生→12×3.14÷3×2=8×3.14=25.12cm
問題③ 解説
点Aが動く場所を図に書き入れると下の図のようになります。
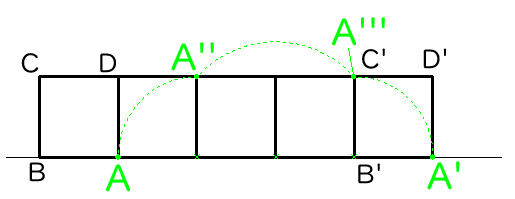
弧AA”、弧A”A”’、弧A”’Aに分けて考えます。
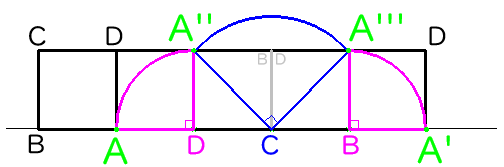
ピンク色のおうぎ形は、下の図のように合わせて考えると、半径6cmの半円になります。
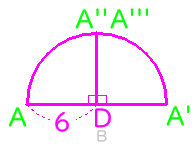
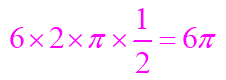
次に、青色のおうぎ形については、半径がわかっていないので、それから求めます。
中3で学習する三平方の定理を用いて半径を求めていきます。
下の図のように、半径は正方形の対角線になるので、1:√2の線分の比の関係から求めます。
(三平方の定理 a2+b2=c2を用いてもOKです)
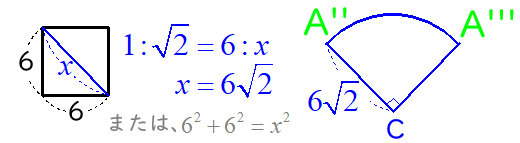
上の図の計算より、青色のおうぎ形の半径は6√2になることがわかるので、弧A”A”’の長さは、
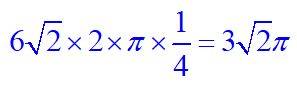
よって、点Aの軌跡は、6π+3√2π=(6+3√2)π (cm)となります。 ※ 3(2+√2)π(cm)
問題④ 解説
- 大きい円(半径6cm)は地面の上を滑らずに回転しています。
- 小さい円(半径2cm)はその上に乗って一緒に回っているだけです。
- このとき小さい円の中心も同じ速さで右に動くので、
小さい円は「地面に対しては回転していない(すべっている)」ように見えます。
👉だから、QQ’ と PP’ の長さは同じになるのです。

移動させているのは半径6cmの円で、その内部にある小さい円の部分は、表面と同じ速さで動いていないため、「引っ張られて動いている(=滑っている)状態にあるということですね。

いかがでしたか。
今回は点が動いた長さの問題としましたが、高校入試などでは、図形が動いた場所の面積を求める問題もよく見かけます。図形の動きがわかれば同様に求めることができるので、チャレンジしてみてください。
高3で数Ⅲを学ぶと解けるようになる問題
半径6cmの円を直線上を滑らないように一回転させる。
点PがP’にくるまでに、点Pが動いた軌跡は何cmになる?
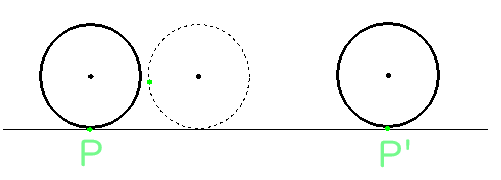

高校で「パラメータ表示」や「積分による弧長の計算」を学んだあと、
発展問題や数学オリンピック・大学入試の難問などで紹介されることがあります。
数Ⅲで学習する内容です。
答えはこちらを開いてください。

”Gemini”に図を読み込ませて、問題文を入力すれば、もう少し詳しく教えてくれます!
点の動きを通して、“全体”を見る目を育てよう
円や正三角形、正方形の一つの頂点を「P」として、その図形を回転させたときにPがどんな軌跡を描くか──。
最初はただの作業に見えるかもしれませんが、このような問題には、数学の本質が詰まっています。
たとえば、点Pの動きを追っているうちに、「あ、ここでも円ができる」「この部分は直線でつながる」といった規則に気づく瞬間があります。これは、部分的な変化を見ているうちに“全体の構造”が見えてくる経験です。

数学の力は、この「部分と全体を行き来する思考」の中で育っていきます。
テストで問われる公式や計算方法は、こうした全体像を理解するための“道具”にすぎません。図形が動くとき、どんな形が生まれ、どこが変わらず、どこが動いているのか──それをイメージできる力は、公式を覚えるよりもはるかに大きな価値を持ちます。
この「全体をとらえる力」は、数学だけでなく、物理や美術、さらには社会の仕組みを理解するときにも役立ちます。
一つの点を見つめながらも、その背後にある全体の関係を想像すること。これは、思考力や創造力を伸ばすうえでとても大切な訓練です。
「点Pの軌跡」という一見シンプルな問題を通して、“一つの点”の動きを超えた“全体の世界”を見通す目を育てていきたいですね。


