【脳葉強化】『三角形の底辺の比と面積の比』 ひらめきラボ《0022》 ~小・中学生のうちから育む「多面的・複合的に考える力」~
今回は、図形の問題。三角形の面積を学習した後であれば、解けますね。(小5で学習します)
ただ、あまり今回のような形式の問題は公立の小学校では扱わないかもしれないです。中学受験する生徒は解けるようにしておきたい問題です。
公立の小学校ではあまり扱いませんが、中学ではできる前提で出題されることもあるので、経験しておくと良いかもしれませんね。
小学生・中学生のうちから育む「多面的・複合的に考える力」はこちらから
では、問題です。
三角形の底辺の比と面積の比
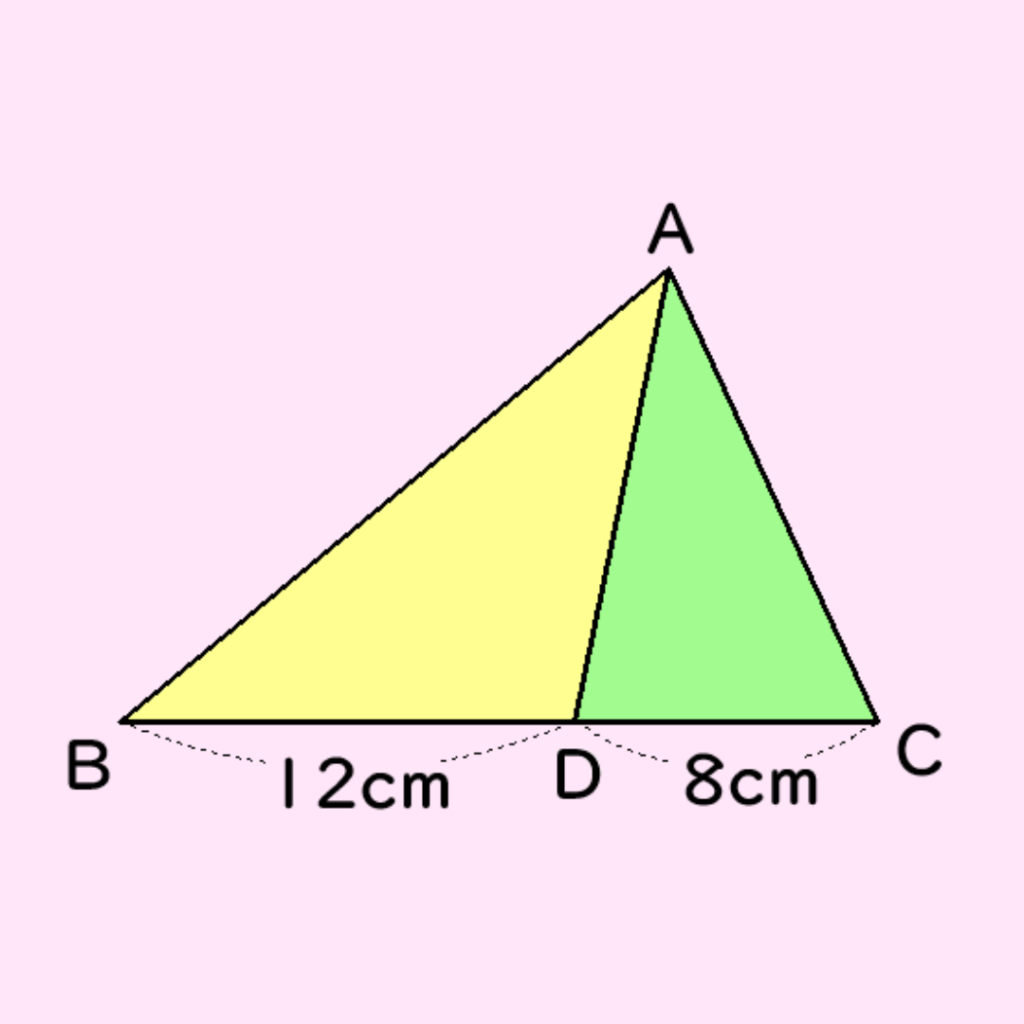
問題1
BC=20cmの三角形ABCがある。辺BC上にBD=12cm、DC=8cmとなる点Dをとる。
△ABDの面積が60cm2のとき、△ADCの面積はいくつ?
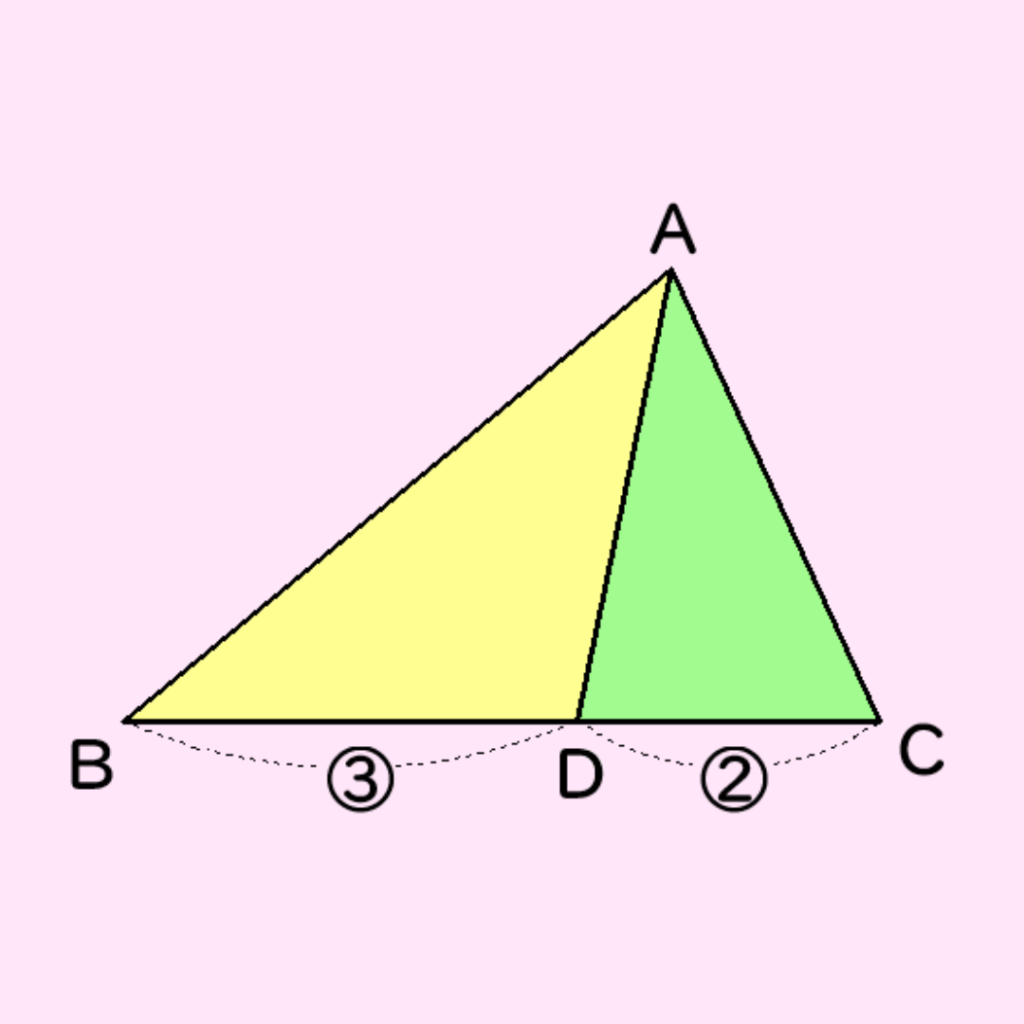
問題2
△ABCがある。辺BCをBD:DC=3:2となる点Dをとる。
△ADCの面積が72cm2のとき、△ADCの面積はいくつ?
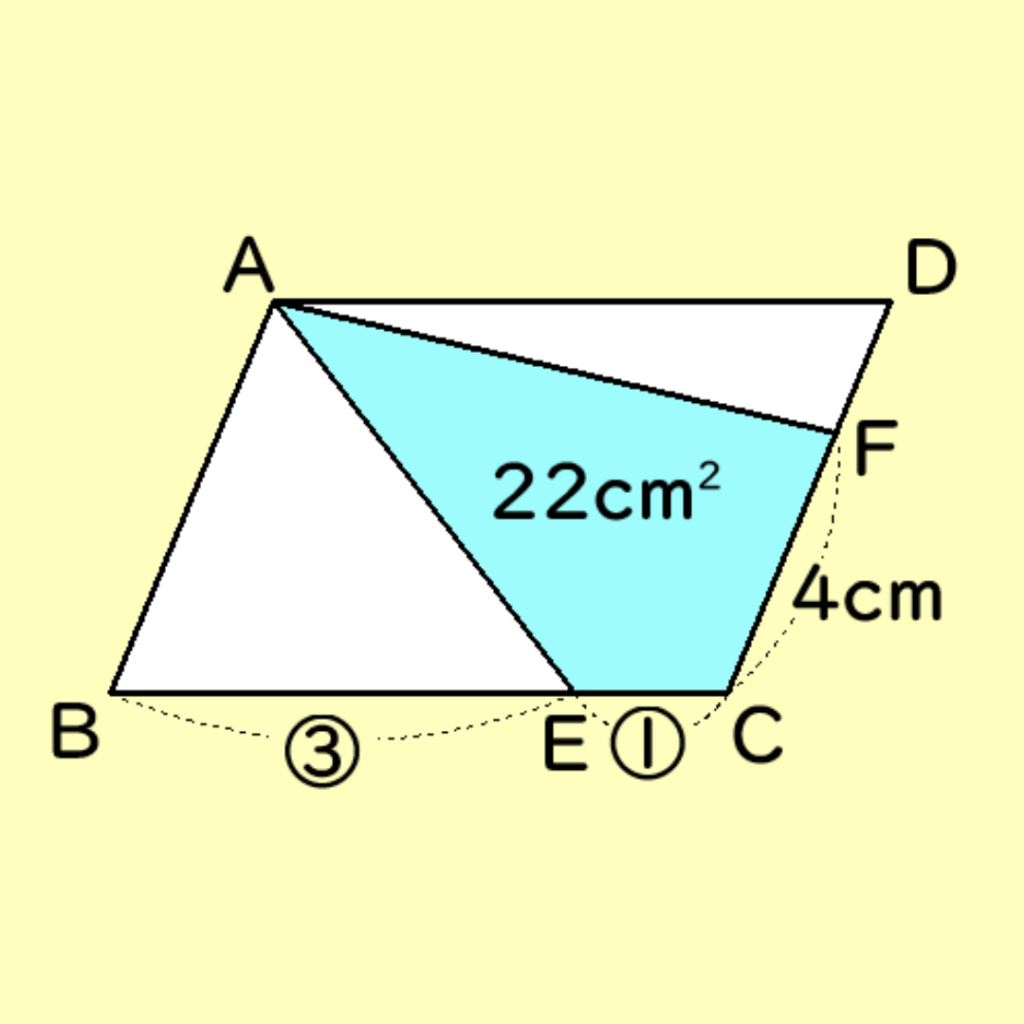
問題3
面積が48cm2の平行四辺形ABCDがある。
辺BC上にBE:EC=3:1となる点Eを、辺CD上にCF=4cmとなる点Fをそれぞれとる。
四角形AECF=22cm2のとき、FDの長さはいくつ?

問題1をヒントに、問題2を考えてみましょう。
問題2を理解できれば、問題3が解きやすくなりますよ。
問題1のヒント
△ABDの面積、底辺がわかっているので、高さを求めてみましょう。
問題2のヒント
問題1から、黄色と緑の三角形の面積の比はいくつになりますか?
これって、底辺の比と・・・
問題3のヒント
2点A、Cを結ぶ線を引きましょう。(補助線ACをひく)
コメント欄に答えや解き方を説明してみよう♪
答えは2ページ目か下のボタンから
「脳葉強化 ~ひらめきラボ~」は、あなたの創造力と思考力を刺激するページです。
斬新な発想力問題や論理パズルを通じて、脳の潜在能力を引き出し、ひらめきの瞬間を体験しましょう。
毎月8日・28日に問題をアップ予定です!


